Introduction
Locks force an algorithm to be sequential during periods of contention. This is a problem when one needs a parallel algorithm because there is guaranteed to be at least one case that forces a locking algorithm to be sequential. If there was no case, the lock could be removed and the algorithm would be the same. For this reason, one might choose to use a lock-free algorithm. A lock-free algorithm eliminates a lot of the contention caused by locking. It handles communication, data sharing, and other mechanisms that usually require threads to be synchronized differently to avoid the need for locks.
On a system using a lock-free algorithm, it is guaranteed that some thread is making progress. This means that the overall system is making progress toward the end goal. However, there still might be starved threads, as lock-free algorithms only guarantee that at least one thread is making progress at any given time.
Compare and Swap
Compare_and_swap is an atomic function. It compares the previous value with the up-to-date value. If they are the same, then it makes the value assignment. Otherwise, the structure has been modified, so the assignment is not allowed.
A traditional compare_and_swap function looks like this:
int compare_and_swap (int* stru_val, int oldval, int newval) {
int old_stru_val = *stru_val;
if(old_stru_val == oldval)
*stru_val = newval;
return old_stru_val;
}
ABA Problem
The first lock-free example involves stack structure. For the push and pop operations, we don't change the stack top until setting up all the new values needed. When we are going to change the top value, the atomic function compare_and_swap is used to check whether the top is the same as it was originally. If it is, then the swap is made. Otherwise, the data structure has been modified by a different thread, so the process must reiterate.
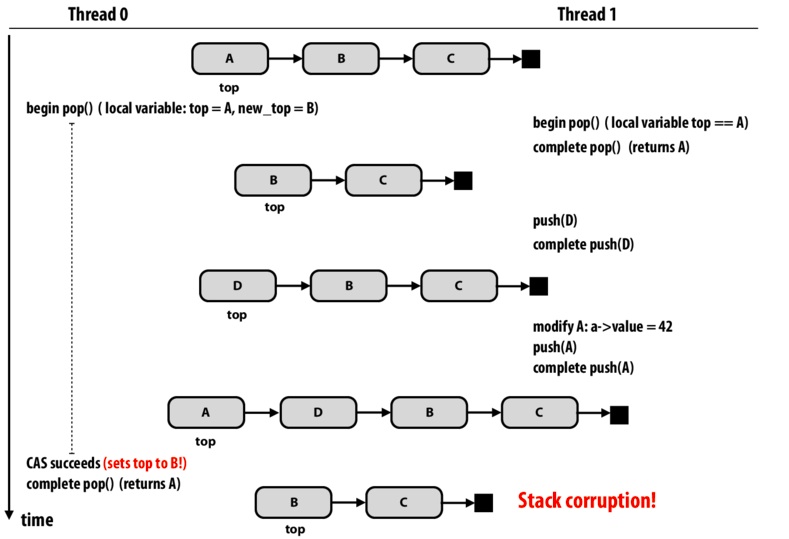
In this first case of a lock-free algorithm, we encounter the "ABA" problem. In figure 1, thread 0's pop operation is interleaved by three operations of thread 1. Thread 0 gets the original top A and the new_top should be B. However, after the operations by thread 1, D is between A and B. Thus, when A is doing compare_and_swap, the top A makes the condition true and then thread 0 sets new_top to be B. This is where the corruption happens, since the top should be D.
Luckily, there are solutions to this problem. One solution is to put a counter for the number of pop operations. By checking both the value and number of pop operations, it can be ensured whether or not the value is up-to-date.
Performance
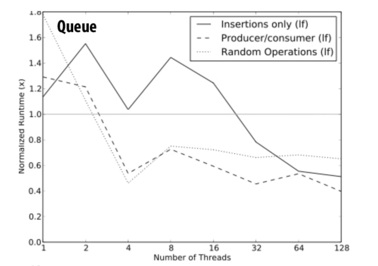
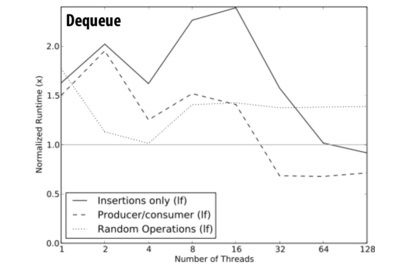
In different data structures, different solutions are required to solve problems. Therefore, the performance results for lock-free algorithms involving different structures are quite different. As seen in figure 2, lock-free algorithms have good speedup in queue structures. In general, lock-free algorithms perform better than those with locking when the number of threads increases.
Questions
- Why is an algorithm that uses locks guaranteed to be sequential in at least one case?
- What is the guarantee that a lock-free algorithm makes?
 nkindberg
nkindbergLock-free algorithms guarantee that some thread will make progress.
This comment was marked helpful 0 times.
- Why do we see a performance decrease for lock-free algorithms on dequeues?
Because if it was possible for the algorithm to be completely parallel, there would be no need for locks. The fact that a lock is used indicates that at some point in the algorithm, only one thread can access a variable at a time, meaning that it is necessarily sequential at at least one point.
This comment was marked helpful 0 times.