Go to the Lecture 4 slides

Steps in creating a parallel program

1. Decompose the problem by identifying subproblems that can be parallelized
2. Assign subproblems to processors
3. Manage communication and synchronization between parallel workers

Here we will focus on the first step, decomposition.

Why do we even have to do this? Why can't the compiler figure it out?

Automatic parallelizing compilation is an open research problem. Given a very simple for loop, like

for (i = 0; i < n; i++) {
    z[i] = x[i] + y[i];
}

an advanced compiler might be able to figure out that there are no data dependencies from one loop iteration to the next and produce a parallelized implementation. For anything more complicated, especially anything that involves dependencies that aren't exposed until run-time, the compiler will not know how to parallelize. So, for the forseeable future, this is your job.

The major part of parallel program decomposition is identifying data dependencies. This can be done either statically before the program is run, dynamically at run-time, or both. Let's look at an example from machine learning: K-means clustering.

K-means

K-means is an algorithm for categorizing data into a pre-defined number of groups (called clusters). It can be used to classify documents, for instance if you have 10,000 blog pages and want to group them into categories such as "clothing," "technology", etc. You can also use it in computer vision to differentiate objects, destroy humans with robots, and accomplish other tasks.

A high-level overview of one version of K-means, known as Lloyd's Algorithm, follows:

1. Choose a value for $k$; this is the number of clusters the points will be divided into ¹
2. Given $n$ datapoints to cluster, randomly select $k$ of those points. These $k$ points are the initial centers of the $k$ clusters.
3. Assign each of the $n$ points to the cluster with the closest center.
4. Recalculate the locations of each of the $k$ cluster centers as the average all the points in that cluster.
5. Repeat from 3 until the change in total intra-cluster distance is less than some epsilon from one iteration to the next. ²

So, the input to this algorithm is some data, usually represented by vectors, and the output is a collection of $k$ clusters of those vectors. An illustration of the algorithm for two dimensional points is shown below.

We are given a data set of points in the (x,y) plane.

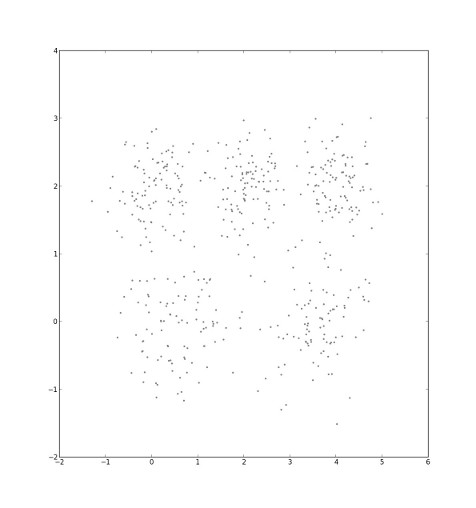
We choose five initial cluster centers at random.

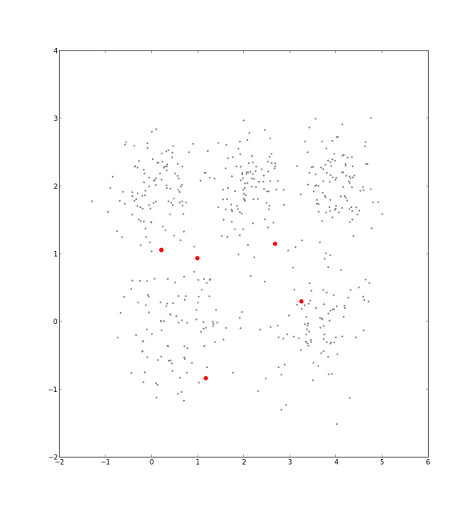
Our selection can be interpreted as the imposition of a Voronoi diagram, in which each point in the set is cordoned off into one sector, that which is nearest to it. Each sector is a cluster.

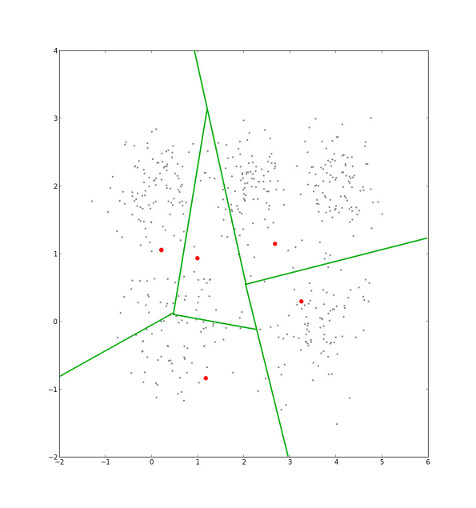
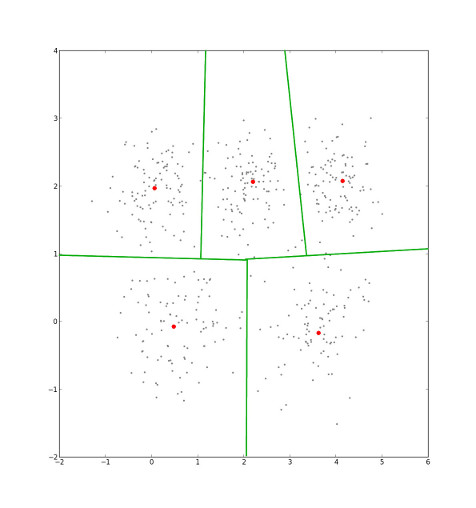
After assigning points to clusters, the cluster centers' locations are recalculated by averaging all the points that are currently in that cluster...

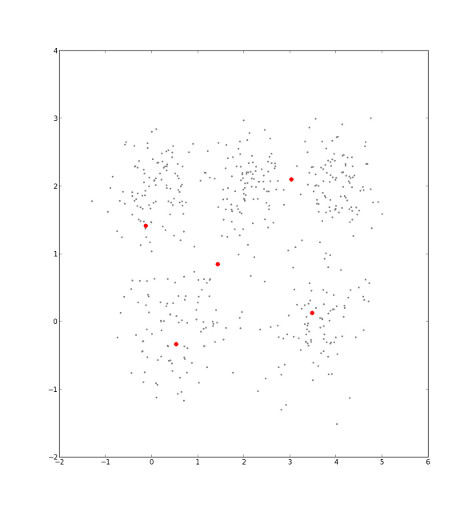
...and the corresponding Voronoi diagram shifts.

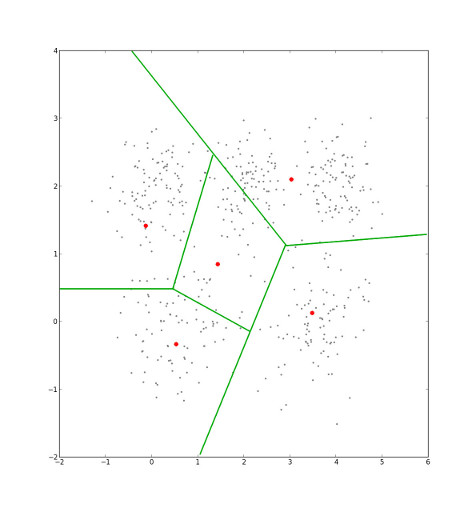
Eventually, the cluster centers' locations will stop changing. When they do, we've minimmized intra-cluster distance, which is the sum of the distance from each point to its cluster center ³.

Parallelizing K-means

There are multiple levels of dependencies in this problem.

The first thing to note is that the cluster assignment and center updating steps will iterate in a loop many times and dominate computation. Each of those two steps is completely dependent on the other; assignment must finish entirely before updating can begin, and updating must finish entirely before assignment can begin again. However, both steps can be individually parallelized.

Assigning clusters to points

One way we can implement this step is as follows:

for 0 to n points:
    for 0 to k clusters:
        calculate the distance from the point to the cluster
    assign that point to the closest cluster

If we have $n$ processors, we can parallelize the $n$ computations in the outer loop of this step. However, each of these loop iterations is parallelizable as well, so if we have $nk$ processors, the entire step becomes parallel (minus the cost of calculating the minimum and assigning to a cluster). (We're talking theoretically here; $n$ might be in the millions, so we probably don't have that many processors.)

Updating cluster centers

We can implement this step like so:

for 0 to k clusters:
    for 0 to m points in the cluster:
        add the point's position to a buffer
    take the average of all points in the buffer and make that the cluster's center

If we have $k$ processors, we can parallelize the $k$ computations in the outer loop of this step. In addition, each loop iteration here is also parallelizable, but not completely. Calculating sums on a shared buffer is not a thread-safe operation, so the best we can do is to calculate partial sums, which can be done in logarithmic time with enough processors.

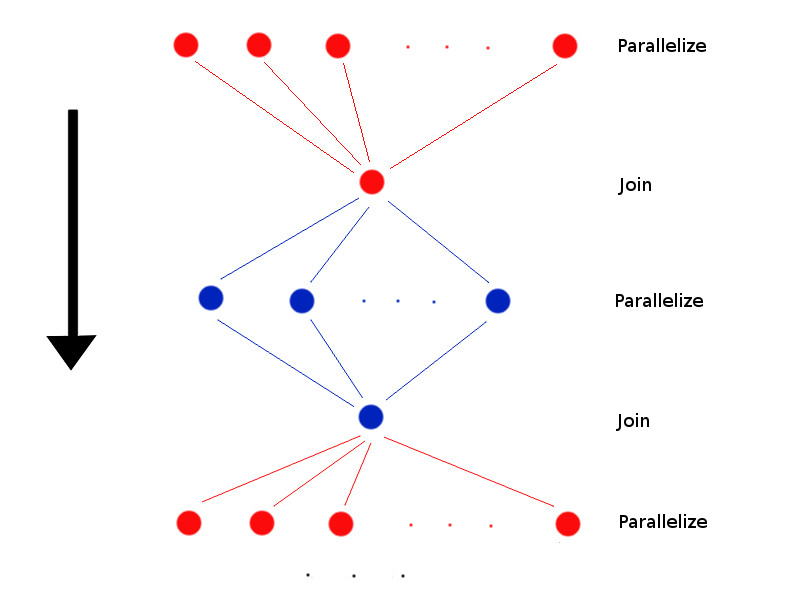
Parallel algorithm

1. Choose k random cluster centers
2. Calculate $n$ distances in parallel
3. Wait until all the processors are done
4. Join the results
5. Calculate $k$ cluster centers in parallel
6. Wait until all the processors are done
7. Join the results
8. Repeat until convergence

Speedup Analysis

How much speedup did we get from this?

It is important to note that the following analysis assumes that there are $p$ processors available and ignores parts of the computation that cannot be parallelized (we'll address this in the next section). We will also look at a single iteration (assign and update), since speeding up one iteration will speed up the whole algorithm proportionally.

The time taken to do one iteration of the serial algorithm is proportional to

$$nk + n$$

where $nk$ is the number of operations spent assigning points to clusters, and $n$ is the total operations taken to go through every cluster's points. The first part can be easily parallelized; there are no dependencies, because each unit of work computes distance from a single point to a cluster center. We end up with $nk/p$ work.

The second part involves averaging all the points in each cluster. You can easily have one processing unit handle one cluster center's recalculation, but computing the average is not so easily parallelizable. This is essentially a big sum, which you can parallelize by doing partial sums on each processing unit, giving you $\log_pn$ run time. Dividing the serial run time by the parallel run time yields the equation below:

$$\frac{nk + n}{\frac{nk}{p} + log_pn}$$

Amdahl's Law

However, not everything in our algorithm is parallelizable. Some components, such as joining results from threads, are inherently sequential. Amdahl's Law gives us a quick method to estimate speedup in this case.

The formula for speedup described by Amdahl's Law is:

$$\frac{1}{(1-P)+\frac{P}{u}}$$

where $P$ is the fraction of the program that is parallelizeable and $u$ is the number of processing units simultaneously working on the parallel section.

The intuition behind this law is that if the parallelizable portion of the problem (what you are speeding up) only occupies a fixed percentage $P$ of the whole, no matter how much you speed up that section you will always be limited to an execution time based on the $1-P$ portion.

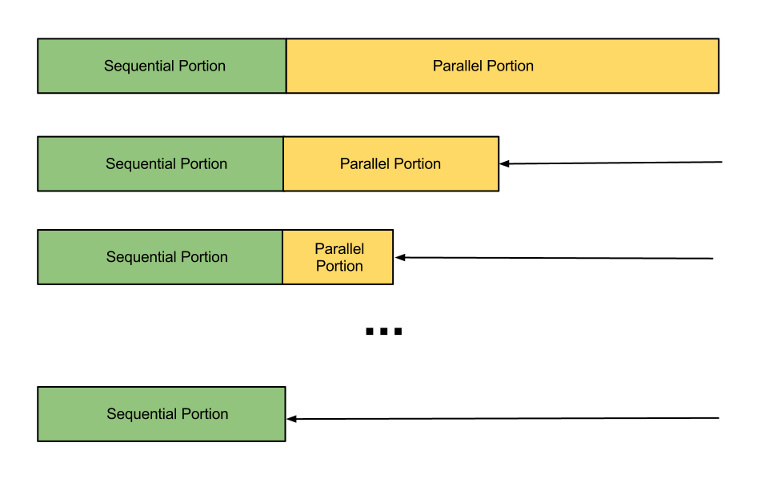
Applying Amdahl's Law

In our parallel K-means algorithm, steps 2 (calculating distances) and 5 (updating means) are parallelizeable, while the other steps are not.

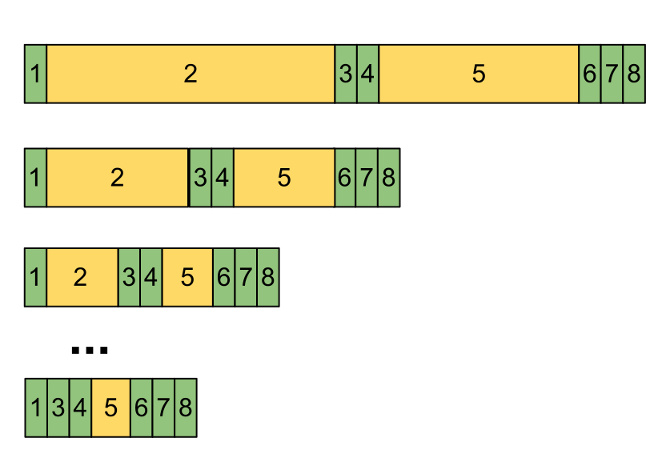
This graph shows that as we add more cores to our problems, our speedup is eventually limited by how quickly we can do the sequential steps. Note hat slice 5 doesn't completely disappear, simply because we can't do partial sums faster than Log(n) time, but it does shrink considerably.

Questions

1. After assigning clusters to points, the program will have some data structure that indicates which cluster each point belongs to. For instance, we could have an unordered list of points with their coordinates and cluster assignment. What could be bad about this when we recalculate the cluster centers?
2. What kind of parallel model does this approach use?
3. Given the parallel model that we chose, are there any adversarial cases to parallelization, or is this algorithm robust to different inputs?
4. What kind of hardware would be a good choice to run this algorithm on a dataset with $n$=1,000,000,000 points?