Blocking vs. Non-blocking
The primary difference between blocking and non-blocking algorithms is which threads are able to make progress in the code execution. In a blocking model, a single thread is allowed to prevent all other threads from making any progress. There is no guarantee that this single thread is making progress itself or that it will ever stop blocking other threads. All locks are blocking, regardless of the implementation. A thread that has taken a lock can prevent others from continuting for an extended period of time for a variety of reasons. Some of these include being swapped out due to OS scheduling, experiencing a page fault, or terminating (e.g. due to a crash) without releasing the lock. On the other hand, a non-blocking algorithm guarantees that there exists a thread that is making progress. However, nothing is specified about which thread makes progress, meaning that starvation is still possible.
Ups and Downs of Lock-free Data Structures
By guaranteeing that some thread will be making progress, you don't have to worry about a single thread preventing the entire program from moving forward. Moreover, the overhead associated with acquiring and releasing locks is eliminated--even when there is no contention, locks still need to be taken and released. However, lock-free code is generally more difficult to write or reason about its correctness. Systems with relaxed memory consistency will also require the use of memory fences in the implementation.
Lock-free Stacks
Stacks make for a simple case study, since the operations on stacks are very simple. The basic principle behind the implementation is that a thread will create a new version of the top of the stack and if no other thread has modified the stack, the change will be made public. However, now the focus turns to how this can be implemented. To accomplish this, a compare and swap (CAS) instruction is required so that the comparison and the write can be done atomically. This instruction is used to check that the top of the stack is not changed in between creating the new top and writing it to memory.
Push
void push(Stack *s, Node *n) {
while (1) {
Node *old_top = s->top;
n->next = old_top;
if (compare_and_swap(&s->top, old_top, n) == old_top)
return;
}
}
CAS is not guaranteed to succeed because another thread may perform its own CAS and change s->top. If this happens the CAS will see that old_top has changed and will try to perform the insert again with the new value. If the CAS succeeds it will push the new head onto the stack, and the push is done. To get reasonable stack behavior, we're implicitly assuming no starvation occurs.
The ABA Problem
Before discussing pop, let's reconsider what our CAS operation is actually checking for: that the top of the stack (the address of the Node, to be specific) is unchanged. This does not actually mean "the stack is unchanged." The ABA problem exposes a case where this isn't a strong enough check. The issue can be exposed with a sequence of push and pop operations.
- Thread 0 begins a pop and sees "A" as the top, followed by "B".
- Thread 1 begins and completes a pop, returning "A".
- Thread 1 begins and completes a push of "D".
- Thread 1 pushes "A" back onto the stack and completes.
- Thread 0 sees that "A" is on top and returns "A", setting the new top to "B".
- Node D is lost.
For a visual showing why the ABA problem exists in a naive implementation, refer to these lecture slides.
Pop
An implementation of pop that avoids the ABA problem can be implemented using a counter to keep track of the number of pops.
Node *pop(Stack *s) {
while (1) {
Node *top = s->top;
int pop_count = s->pop_count;
if (top == NULL)
return NULL;
Node *new_top = top->next;
if (double_compare_and_swap(&s->top, top, new_top, &s->pop_count,
pop_count, pop_count + 1));
return top;
}
}
Here, a double-CAS is used to update both the stack and the counter, only if both are unchanged. This defeats the ABA problem outlined above because in step 5, thread 0 would see that the counter has changed even though the top has not and will start over. One remaining issue to consider is how to handle when the counter reaches the limit of its type.
Hardware Support
While the code in the previous section is valid, we have not considered how compare_and_swap as well as double_compare_and_swap are managed. The reason that we need them in the first place is that the operation must be atomic. To permit this, x86 has dedicated instructions for CAS on 8 and 16 bytes of data, cmpxchg8b and cmpxchg16b. Note that to perform a double CAS the relevant data must be in adjacent memory and then perform a 16 byte CAS, further adding complexity to lock-free data structures.
Linked Lists
Implementing a lock-free linked list uses the same idea as stacks, but with the added complexity of operating on any position in the data structure.
Insert
To implement insert, you first need to find the correct position in the list. Assume we have found this location and that we're inserting Node *n after Node *p. The insertion code is
while (1) {
n->next = p->next;
Node *old_next = p->next;
if (compare_and_swap(&p->next, old_next, n) == old_next)
return;
}
The operation that we need CAS for is to update the next pointer for the node we're inserting after (*p) to ensure that another thread hasn't modified the same position. This process is shown below.


Deletion
As we saw with stacks, allowing for a second operation (pop) complicated the implementation. With linked lists, simultaneous insertion and deletion is not easy to account for. If we have "A"->"B"->"C", a problem case would be
- Thread 0 begins to delete "B" from after "A".
- Thread 1 begins to insert "D" after "B".
- Thread 1 points "B" to "D".
- Thread 0 points "A" to "C"
- The delete operation removed "B" and "D".
To fix this, there must be a way to ensure that "A" is also unchanged when inserting after "B" and how to react when this happens.
Performance
As we saw in lecture, lockfree data structures don't necessarily show better performance, despite the apparent benefits. Performance is particularly bad with a dequeue. In cases where a CAS operation will fail many times before succeeding, you end up doing a lot of extra busy waiting, similar to a spin lock. For this reason, higher contention is less favorable for lock-free operations, as evidenced by the insertions only examples in the lecture slides. It is also interesting to note that in a linked list, fine grain locks don't necessarily perform better than the pthread mutex lock. In these cases, the overhead of acquiring/releasing locks is too large for small and large processor counts.
Review Questions
Give an example of a programming setting where lock-free data structures would be extremely beneficial and why.
Could the test-and-set atomic primative be used instead of compare-and-swap to create a lock-free data structure? Why or why not?
A natural first attempt at lock-free delete in a linked list would be to perform a CAS with the pointer to the element to be deleted and it's next node. For example, this would be the result from removing 10:
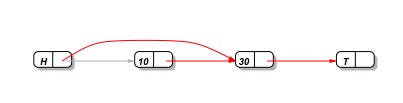
However, using this the following situtation can arise: ![ll-4http://15418.courses.cs.cmu.edu/spring2013contentnt/article_images/46_4.jpg)
Explain how this can happen with a single CAS and why it is a problem for correctness of the delete operation.Refering to the previous issue of question 2, some modern lock-free linked lists use 2 CAS operations per delete. What would each CAS operation be responsible for? How does this solve the problem highlighted by problem 2?