

To further get a sense of all the things that GraphLab helps make easier, checkout the image that they have on on this page. Basically they already have MPI, pthreads, and Hadoop as methods of taking advantage of parallelism either across multiple machines or within one machine. Also though they have a lot of support for graph algorithms, they also have support for computer vision (Image Stitching is really cool) and clustering.
This comment was marked helpful 0 times.


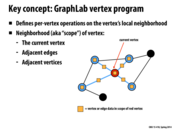
As mentioned in class, a good way to think about an operation like this is as a shader in OpenGL. Shaders compute the value of a particular mesh element given specific input data (ie color of vertex, colors of neighboring vertices, value in a uv texture map, etc). Here, we are using the values of the neighboring vertices (the in-neighbors) of a vertex to compute the rank of the vertex.
This comment was marked helpful 0 times.

@arjunh - That is a good analogy. The per-vertex kernel (analogous to a shader program) is essentially the inner block of a for loop that is called by the runtime, probably in parallel. I think that this "thinking like a vertex"* approach is used in both Graph Lab and in Google's Pregel.
This comment was marked helpful 0 times.


I'm going to attempt to explain the functions on this slide just to make sure I understand GraphLab's abstractions.
The gather_edges function simply defines the edges (for each vertex) on which gather is called. The gather function is called on each of the defined edges and each of these calls is reduced with the addition operator and stored in the argument "total" in the apply function. The apply function updates the value at each vertex (presumably using "total", the result of the gather reduction). Finally, the scatter_edges function pushes the updated value of each vertex to the defined edges.
This comment was marked helpful 0 times.


Signaling is useful in the case where some parts of the graph converges faster than others. Their will be no need to refine all the areas of the graph in that case. The next slide explains the implementation in more detail.
This comment was marked helpful 0 times.
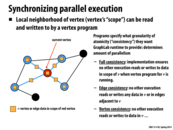

What's an application where writing to adjacent vertices wouldn't be okay but writing to adjacent edges would be? I'm kind of confused by vertex consistency vs. full consistency
This comment was marked helpful 0 times.

The way I interpreted vertex consistency from this slide was that vertex consistency would make sure nothing was modifying the data in your current vertex in parallel.
Summarizing the definitions in terms of the picture,
- Full consistency: Nothing else is modifying anything marked by a yellow box.
- Edge consistency: Nothing else is modifying the red node or edges coming out of it.
- Vertex consistency: Nothing else is modifying the red node.
This comment was marked helpful 1 times.

Actually, the definitions specify that not only is nothing allowed to modify the neighborhood vertices/edges/both (depending on the type of consistency), but nothing is allowed to READ from them either. So one situation where you might want consistency on the vertices but not on the edges is if the information on the edges isn't changing, and it is only being read. Because then it wouldn't matter if multiple programs were looking at it at the same time. The same would be true if you were only updating edges and not vertices. This is a really simple example, but there are probably other examples where both are being modified but you only care about consistency in one of the sets.
This comment was marked helpful 2 times.

Not specifically specified but implicit is the null consistency, which has no restrictions on modifying anything.
This comment was marked helpful 0 times.


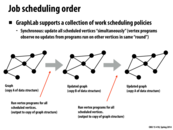
Kayvon said that the ability for the user to customize scheduling policy makes GraphLab an "unclean" abstraction. Doesn't GraphLab also take care of scheduling if the user does not provide a policy, just like Lizst? I guess what I'm asking is why does having a clean abstraction matter if we know that whatever scheduling policy Lizst/GraphLab tries to come up (in some cases) will not be as good as the scheduling policies we put in place. Because like the slide says, this is common and necessary in designing efficient/fast algorithms.
This comment was marked helpful 0 times.

I don't think that Kayvon implied that a clean abstraction is necessarily better - he was probably just pointing out the differences. Having a clean abstraction allows the user to not have to (or, makes the user unable to) worry about implementation details. It would be 'cleaner' and more representative of what is trying to be accomplished. On the other hand, an unclean abstraction allows users more flexibility in optimization.
This comment was marked helpful 2 times.


Graph Lab implements the MapReduce Abstraction through an Update Method which is the "per-vertex update" and a sync function which is the "global reduction". The Update function is able to read and modify overlapping sets of data/program state in a controlled fashion through "powerful scheduling primitives". The GraphLab site is here: http://www.select.cs.cmu.edu/code/graphlab/
This comment was marked helpful 0 times.

What does lazy execution mean??
This comment was marked helpful 0 times.

I believe lazy execution is waiting to evaluate an expression until the value is needed, and also tries to do sharing of values for repeated expressions as much as possible.
This comment was marked helpful 0 times.


The common sense of BFS is find the nearest parent of each node from the root, however, I'm not sure how this algorithm make sure this happen. Maybe the further node may execute faster than nearer node, as it doesn't have super step as Pregel does.
This comment was marked helpful 0 times.

@black This algorithm follows the typical BFS algorithm. It uses a frontier to traverse the graph deepening its search each iteration. We can see this sequential loop in the BFS procedure. Every time the EDGEMAP procedure is run the frontier moves 1 edge farther away from the root.
This comment was marked helpful 0 times.


I understand that visiting an unvisited node is useful work, and that traversing an edge that points to a node visited via another edge in this same step results in more edges to traverse than necessary (so that additional edges pointing to the same node result in unnecessary work). Which of peers and valid parents are considered wasteful?
This comment was marked helpful 0 times.

@cardiff, I think this slide means only claimed child is useful since those are what we want from the frontiers. So failed child, peer, and valid parent are all wasteful.
This comment was marked helpful 0 times.


EDGEMAP_SPARSE and EDGEMAP_DENSE correspond to bfs_bottom_up and bfs_top_down that we have implemented in Asst 3 Part 2.
This comment was marked helpful 0 times.

@taegyunk, I think it is the other way around. bfs_bottom_up would deal with all the vertices in parallel, so it is EDGEMAP_DENSE. bfs_top_down deals with frontier elements in parallel, so it is EDGEMAP_SPARSE.
This comment was marked helpful 0 times.

I agree with @yanshan2, EDGEMAP_DENSE would correspond to bfs_bottom_up, because we iterate over every vertex. EDGEMAP_SPARSE would correspond to bfs_top_down because we only consider the frontier. As we noted in the assignment, bottom up was more efficient when we had a large frontier. Therefore, when the graph is more dense, it makes more sense to use a bottom up step, where we check every vertex.
This comment was marked helpful 0 times.


One way to do this requires a few changes. First, we can swap the order of all edges in the graph. This is necessary in order for the next change to make any sense. In PRUPDATE, I believe we should swap d and s, as we want any vertex that is doing work to keep updating. Thus, any vertex which is active will increment its page rank by using the values of its neighbors.
I believe the other change which is needed is to change COND. We could replace it with "return (diff[i]>eps2)", thus when the difference is less than some epsilon, this vertex will stop updating its own value.
In this implementation, each vertex is responsible for its own updates, so removing a vertex after it converges will not cause other vertices to lose data that they needed to continue updating.
I believe this should work, however it does require making a new version of the graph which I am not sure is possible and in fact may cost more than the savings of this method.
This comment was marked helpful 0 times.

I think the convergence is a global state. If one node is converged at some time, it stops to iterate. But some far-away node might pass some weight to this node in the future, and the node's weight need update at that time.
So is it acceptable to stop iterating for some single node?
This comment was marked helpful 0 times.


The below is a pdf to a paper by the Stanford developers of Green-Marl, explaining the DSL fully. The optimizations, the type of data structures and the implementation fully.
Green-Marl: A DSL for Easy and Efficient Graph Analysis
This comment was marked helpful 0 times.


For those interested in pregel here is an overview: http://googleresearch.blogspot.com/2009/06/large-scale-graph-computing-at-google.html
From the overview: "In Pregel, programs are expressed as a sequence of iterations. In each iteration, a vertex can, independently of other vertices, receive messages sent to it in the previous iteration, send messages to other vertices, modify its own and its outgoing edges' states, and mutate the graph's topology"
This comment was marked helpful 0 times.

I found another one called GraphX, which seems interesting. From their website: "The goal of the GraphX project is to unify graph-parallel and data-parallel computation in one system with a single composable API." It also has quite a large set of operations.
This comment was marked helpful 0 times.


From my understanding (since I don't believe it has yet been explained in the slides), streaming refers to performing computation on a graph dynamically, rather than statically (in memory). Usually (from internet searches), streaming refers to small changes in a large graph which are unrelated, and thus provide a constant "stream" of new data for analysis. However, in this case, streaming can also refer to when we do not have enough memory to hold the entire graph (and so we must constantly pull our information about different sections of the graph from memory as a stream).
This comment was marked helpful 0 times.


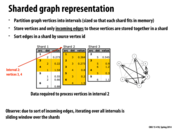
Here, sharding is used on a directed graph. This method can be adapted to an undirected graph by creating a directed graph where every edge goes both ways. You only need to read a single shard then to obtain all information about the vertices in that shard. This method of course comes at the expense of space since every undirected edge has to be stored as two directed edges. Is there a more efficient representation for streaming undirected graphs?
This comment was marked helpful 0 times.

Here, the point of this data structure is to maximize disk utility when performing operations that only require a vertex's local neighborhood. Since the entire graph cannot fit in memory and random disk access is VERY expensive, we want to organize the graph into these intervals, so disk access pattern is more predictable (contiguous).
One other interesting thing is how this approach compares in terms of performance and complexity of that of using distributed systems. Sure, failure tolerance and consistency is a pain in the ass for the developer who writes the framework, but the end user won't feel much difference (since using DS underneath a language like Ligra would actually be a reasonable implementation, I think). Also, as we saw with web servers, hitting disk is worse then hitting network and accessing a in-memory cache. Anyone else have an opinion?
This comment was marked helpful 0 times.

@uhkiv, I agree a DS approach is likely better suited for this type of computation. It seems like the problem is almost entirely memory bound, which network latencies can easily trump disk latencies on. But as was stated in an earlier slide, the motivation behind this approach was because clustering machines is difficult/expensive.
This comment was marked helpful 0 times.

Are there cases where the structure of the graph leads to sharding with very uneven shard sizes, diminishing the benefits of this technique?
This comment was marked helpful 0 times.

Well from this article, it discusses how finding an ideal distribution of a graph onto many different memory banks is a difficult task and how different distributions of the same data can vastly change the communication overhead of computations on the graph:
http://jim.webber.name/2011/02/on-sharding-graph-databases/
This comment was marked helpful 0 times.

Is it possible to sort edges by value (or some key in general)? Does sort by source vertex id have other impacts? One thing I can think of is that destination vertices can be loaded faster but that does not seem to apply to sparse graph.
This comment was marked helpful 0 times.



















This paper has more information on the implementation of PageRank with MapReduce, including its shortcomings, and optimizations that can be made to improve performance. MapReduce is often a bad fit for (iterative) graph algorithms simply because it was never designed with them in mind (e.g. the original paper never even discussed them). In the case of PageRank, using MapReduce involves passing a lot of data back and forth, which dominates runtime.
This comment was marked helpful 0 times.
Continuing the point above, since map-reduce uses a message passing model, data needs to be sent over the network between nodes, therefore if there were a lot of data to be sent, it will be costly.
This comment was marked helpful 0 times.