

Note that there is still a cost for each region reporting its results back to the respective home regions involved in each computation, since the results are computed in a "neutral" region.
This comment was marked helpful 0 times.

It turns out that D.E. Shaw developed a machine called Anton specifically designed for computing molecular dynamics simulations. It uses the NT Method (and ASICs!) and is described here
This comment was marked helpful 0 times.

It's also discussed briefly in the lecture on heterogeneous and specialized processing.
This comment was marked helpful 0 times.


What confused me about this is the meaning of the import region for $P$. Aren't $A$ and $B$ (and other particles in the import region of $P$) at a distance of more than $R$ apart? They could be as far as $\sqrt 2 R$ apart it seems.
This comment was marked helpful 0 times.

Yes, A and B are more than distance R apart from each other if you were to draw a straight line between them. However, one of the ideas behind neutral territory is that when A and B are interacting, you don't have to import everything in the space between them. So, you only have to import the rows and columns that actually contain A and B. Since A and B are distance R from P, you only have to import data up to distance R away from P in 4 directions. In each of these 4 directions, the area is bR. Then the $b^2$ comes from the yellow region that is already on P. That is why the size of the import region is $4bR + b^2$. It doesn't matter how far A and B are from each other, only how far each of them is from P.
I think this is what you were asking about... Is this explanation correct?
This comment was marked helpful 0 times.

It kind of seems to me like moving to the same x/y square is... somewhat arbitrary? Would there be any potential advantage of this mechanism over, say, hashing the combination of an ID of "A" and "B", to consistently process the interaction between A and B on an effectively random processor?
This comment was marked helpful 0 times.

I'm not sure, but I think selecting the x/y square would improve spatial locality over simply selecting a random processor. For example, if we had a mesh interconnect on the above slide, A and B would only be two links away from the yellow square. But if we had selected a random processor, chances are that that processor would be much further. Choosing the x/y square reduces the latency of communication between processors. Can someone verify this?
This comment was marked helpful 0 times.

Question: Why is the import region of the yellow square just the blue regions? Wouldn't it be all pairs of points where the first point has its X coord in the blue row and the second point has its Y coord in the blue column?
This comment was marked helpful 0 times.

@spilledmilk: that would only be the case if the range were infinite - there are many pairs satisfying your description whose points are too far away from each other, so we need not communicate all of those points to the yellow square.
This comment was marked helpful 0 times.

@spilledmilk: If you're asking why it is not the whole row and the whole column, it is because we are not considering interactions beyond the specified radius.
Also I think it should be the first point with X coordinate in the blue column, and Y coordinate in the blue row
This comment was marked helpful 0 times.

@sbly @jmnash Is part of the interaction computation checking the distance between the points? If so, it seems like the motivation behind this is that processor P will have to pull both A and B into memory anyway, so you might as well check their interaction with each other while you have them. This way, the pair (A,B) is only ever loaded by one processor.
This comment was marked helpful 0 times.


The intuition that made sense to me was that in each processor, every particle being computed is being reused in up to 4 areas in a single processor, whereas in the previous radius example, only the center particles are being reused within a single processor.
This comment was marked helpful 0 times.
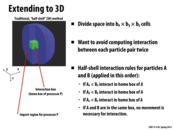

There are a few other methods that can also be competitive in terms of the communication/computation ratio. One interesting one is the foam method, which takes a bunch of 3D regions out of the half shell (and makes the 3D representation look like a bunch of floating bricks). 1 particular study (KJ Bowers, 2005, Overview of Neutral Territory Methods) found that the foam method is as good as Shaw's neutral territory (shown in the next few slides) as the number of processors increases.
Another interesting one is the eighth shell method, which just takes an eighth of a shell. The same study found that for small numbers of processors, the eighth shell method is better than Shaw's neutral territory.
This comment was marked helpful 0 times.


I was wondering why this wasn't a 3-tower shape. This makes sense because there are 3 dimensions but only 2 points interacting. So you must take 2 coordinates from one and 1 from the other.
This comment was marked helpful 0 times.


How does the NT method correspond to constant communication?
This comment was marked helpful 0 times.

There seem to be a variety of ways to implement the "neutral processor", and implementations have different advantages depending on number of particles and processors. A related paper: http://iopscience.iop.org/1742-6596/16/1/041/pdf/1742-6596_16_1_041.pdf
This comment was marked helpful 0 times.


How would Cilk be implemented? We talked about that it is different from pthreads in that it does not have context switching overhead and does not decrease locality for cache. My understanding is that Cilk has #threads = #cores, and threads get work from work pool concurrently. Although we may have multiple spawns, maximum number of threads is fixed. Is this right?
This comment was marked helpful 0 times.
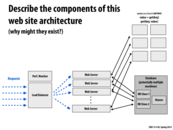

The load balancer, combined with the performance monitor, directs requests to servers. This is necessary because when we have multiple servers, we want to make sure we're using each one as fully as possible. Thus, it's useful to have a component that, for example, prefers to send jobs to servers with empty queues rather than servers with other requests queued up.
We need at least one web server in order to be able to generate responses to requests. This may involve loading data from the database, storing data in the database, performing a calculation, or pretty much anything a server can do. We want multiple servers so that our web site has low latency even given lots of simultaneous requests, so that we can efficiently process requests concurrently.
We want a database because files stored in a normal filesystem aren't organized as optimally as they could be. Database allow us to optimize for specific patterns of reading/writing (e.g. tables or indexes in SQL databases). The database has multiple slaves and one master so that multiple reads (from slave DBs) can occur concurrently, while writes have to be processed by the master DB (and propagated to slaves). This allows reads (which are much more common) to occur efficiently, while still ensuring eventual consistency.
Finally, we have memcached servers because even with a highly optimized database, reading from a DB is generally the slowest part of generating a response. Thus, we want to cache the most frequently accessed data in memcached to ensure low latency. We can also use memcached to cache pretty much anything, such as expensive computations or page renderings.
This comment was marked helpful 5 times.

Note that this particular DB implementation makes use of replication of data. This is particularly useful because most applications have many more reads than writes and we also are okay with relaxed consistency on read/write ordering. For use cases where writes are about as common as reads, or space might be more limited, partitioning the database is viable as well.
This comment was marked helpful 0 times.


The ABA problem is when the assumption is made that nothing was done because consecutive reads gave the same value. However, another thread could have modified the data, performed a computation, and then changed it back, so something did happen. We saw this problem when deleting elements from a linked list. A nice description can be found on the wikipedia page.
This comment was marked helpful 0 times.
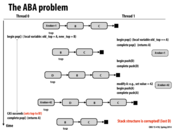

A major problem with lock-free implementations of many data structures is illustrated on this slide. Although they provide alternatives to locks such that more than one thread can be acting on the synchronized section, lock-free data structures also are difficult to reason about. Here, the correctness of the lock-free implementation depends on not using the same node once again as part of the stack. This could be taken care of by policies that require the use of a new allocated node each time something is inserted into the stack, but that requires extra restrictions/effort on the part of the person writing code that uses such data structures.
This comment was marked helpful 0 times.


Question: In class a clever, but not-to-be-publicly named student found a bug in my initial implementation, which is now fixed. The original version of pop() flipped the order of the first two lines. The buggy version is below:
Node* top = s->top;
int pop_count = s->pop_count;
Can someone describe why (give an example) of how this buggy implementation fails?
The original slide in the lock-free data structures lecture has also been fixed.
This comment was marked helpful 0 times.

Say we have two processors, $P1$ and $P2$, and the top of the stack is node $A$. In the buggy version, $P1$ executes line 1, grabbing a pointer top to $A$. Then before it executes line 2, $P2$ changes the stack, but $A$ still ends up as the head of the stack (ABA problem). Then P2 executes line 2, and gets the pop_count for the corrupted stack. Assuming $P2$ does nothing else in the meantime, $P1$ finishes pop() and the CAS passes because pop_count hasn't changed and $A$ is still the head of the stack. However, the stack has changed since $P1$ got a pointer to $A$, so the results are incorrect.
This comment was marked helpful 0 times.

I still do not see why this is a problem. For @sbly's explanation, I do not understand why P2 executes line 2 after it changes the stack. If P2 changes the stack, it would have executed the pop function successfully for at least once, so the count is already changed, then why P2 is necessary to call the pop function again? I do not see the meaning of this.
Also, even though A is still the head of the stack, why the result is incorrect?
This comment was marked helpful 0 times.

@kayvonf Although I do understand why the buggy implementation is buggy, I'm not sure if I can produce a scenario where the buggy implementation's behavior would be different from the modified version's. Because we grab new_top after we grab pop_count, I don't think we can get a situation like the last slide's. Can anyone produce a scenario where the two implementation will behave differently?
EDIT: I actually went to @kayvonf's office hours to discuss this, and here's what we figured out:
Let's say we have the buggy implementation in play here. Observe the following stack: A - B - C s->pop_count = 0
P1 comes into pop, and set its local variable top to A. Note that pop_count is still zero. Then, we context switch to P2. P2 pops A (pop_count is now 1), pushes D, and pushes A back in to the stack again. So, the stack is now A - D - B - C s->pop_count = 1
We resume the execution of P1, going to line int pop_count = s->pop_count, where we set P1's local pop_count equal to 1. HOWEVER, we now go onto say new_top = top->next; which IS actually D.
So, in conclusion, we figured out that as long as we have the int pop_count = s->pop_count BEFORE we grab new_top, we won't be able to corrupt the stack like the last slide.
It would be interesting to find a situation where the buggy implementation and the non-buggy implementation actually have different results, as I mentioned before the EDIT.
This comment was marked helpful 1 times.


The pop count is at a different address from the top, so the top could be updated and then set back to its original value by another processor (classic ABA problem), but the pop count not yet updated (since it had not yet been flushed to memory from the other processor's cache). Then when the first processor looks at pop count, it does not see the changes made by the other processor, so it proceeds to perform the double compare and swap, and the ABA problem occurs leading to corruption of the stack.
This comment was marked helpful 2 times.





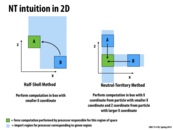








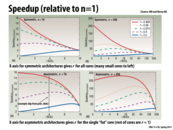




Relating to Problem 2A. from sample exam questions,
Question: how would the topology of an interconnect affect the performance of above computation?
This comment was marked helpful 0 times.
Basically the mesh interconnect system basically exactly fits this problem. Each processor would take the cell that matches with its position in the interconnect and then each processor will only have to communicate with other processors that are 1 link away from them.
This comment was marked helpful 0 times.
Analyzing the different interconnect begins with the analysis that the computation on one data point on a processor will most likely require communication to processors that are surrounding on all cardinal directions.
In an interconnect system like the ring interconnect, the structure does not match the communication pattern of the program. We will have to wait 16 complete ticks for data to leave one processor, arrive at the next processor, and go back to the start.
On a a grid interconnect, this is limited down to 4 for any processor that is one cardinal direction away (assuming proc location influences data point distribution).
It all comes down to matching a communication pattern with an interconnect
This comment was marked helpful 0 times.