

C++'s classes offer a safer way of dealing with remembering to unlock the mutex. For example, Boost provides the boost::scoped_lock template. It's a class which wraps a mutex. Its constructor locks the mutex and its destructor unlocks the mutex. This guarantees that the mutex will end up being unlocked when we leave the function, whether that be by returning or even throwing an exception:
void insert(List *list, int value) {
boost::scoped_lock<boost::mutex> lock(list->lock);
... Rest of the code, with no explicit unlocks ...
}
The lock variable goes out of scope when the function returns (or an exception causes the stack to unwind past this function call), causing its destructor to be called which unlocks the lock.
This comment was marked helpful 0 times.

Note from @thedrick in class: The second unlock in the delete function should be outside of the while loop.
This comment was marked helpful 1 times.

Protecting the entire linked list with one lock does not do well for parallelism. By locking the list, you are unable to add or delete anything from it in another thread. This approach would work pretty well if a lot of your operations are read-only, but with a high number of write operations, this would probably be slower than a serial version with the overhead of locks.
This comment was marked helpful 0 times.
@sfackler: is this like a synchronized in Java?
This comment was marked helpful 0 times.

We can do much better than using one lock but locking individual elements of the linked list based on the dependencies for insert/delete. This will allow us to ensure parallelism for these operations while avoiding data corruption..
This comment was marked helpful 0 times.


The idea to ensure correctness here is to treat insert/delete operation as a transaction.
Whenever the operations are executed, the data used for operations is protected from interference of other concurrent operations. The method of this is to lock all currently related resources in each step.
The implementation here locks and only locks necessary resources for current or following steps. So it is a perfect implementation in the frame of this idea.
This comment was marked helpful 1 times.

In this implementation each thread uses locks to ensure it has exclusive access to its prev and cur nodes. This is a much better solution than maintaining exclusive access to the entire linked list for a single thread.
This comment was marked helpful 0 times.

@aakaskr: The solution certaining enables a high degree of concurrency when operating on the data structure. Whether the solution is in fact better than a coarse-grained locking solution depends on many factors, such as the number of contenting threads and the overhead of manipulating the fine grained locks. For example, in the transactional memory lecture, there is a slide showing an example where performance degrades when using fine-grained locks.
This comment was marked helpful 0 times.
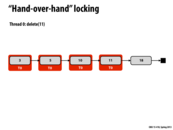

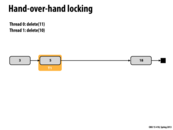
In lecture this slide showed an animation of the red blocks moving along the linked list as a group of two, where each subsequent step involved the far left red section to move to the next available cell on the right. This is the idea of "hand-over-hand" locking which ensures write operation integrity. Since the list must be traversed from left to right, you will only have access to an element if you have locked it's cell and those cell's that are dependents.
This comment was marked helpful 0 times.
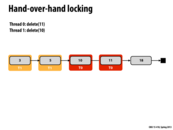

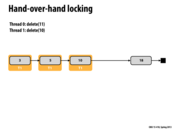
Here we can delete element 18 without grabbing its lock. This is because for another thread to delete element 18, that thread must hold the lock on 11.
This comment was marked helpful 0 times.

In this example, a thread iterates over the linked list by placing a lock on the previous and current nodes. Every time the thread wants to moves to the next, it places a lock on next node, removes the lock on the previous, and moves.
When thread 0 tries to delete element 11, it won't run into the problem of element 18 being deleted, since a thread needs the lock on the previous node before it can delete the current.
This comment was marked helpful 0 times.

Each thread only lock the prev and curr node which are currently iterating, then the unlock node can be deleted by other thread without any effect at all.
This comment was marked helpful 1 times.


Before we added locks traversing the list only required read operations. Now that we must have a lock for every node and previous node we access, even traversing the list without modifying it requires memory writes.
This comment was marked helpful 0 times.

We know immediately that linked list code is deadlock free because all the threads that traverse the linked list acquire and release locks in order. Hence, there cannot be a circular dependancy.
This comment was marked helpful 1 times.

A middle-ground solution is to have locks equally spaced with k nodes apart. Then the overhead of taking/releasing locks and storage cost is reduced by a factor of k.
This comment was marked helpful 0 times.


Invariants: -Consumer moves head -Producer moves tail -Producer handles all memory allocation and removal
This comment was marked helpful 0 times.

The trick here is that we have another 'head pointer', the 'reclaim' pointer. Consumer drops elements from pointer 'head' by move the 'head' pointer forward. Then the dropped elements will be hidden from consumer. But they can still be accessed via the 'reclaim' pointer. So, the producer can know which element is deleted and do both allocation and deletion.
This comment was marked helpful 0 times.

The reclaim node pointer in queue is the key of implementing this lock free queue data structure. The producer takes advantage of the reclaim pointer to issue the allocation and deletion in the queue.
This comment was marked helpful 0 times.


blocking algorithm serialize the access to a data structure and therefore should be avoid the in design of algorithm if possible.
This comment was marked helpful 0 times.


Since some thread is guaranteed to make progress at any time, lock-free algorithms allow for "perfect" parallelization. Algorithms that use locks can, at some point, block threads because of contention on the critical section, forcing the algorithm to be sequential for that moment.
This comment was marked helpful 0 times.

We looked at a lock free priority queue for our final project (based on http://www.cse.chalmers.se/~tsigas/papers/JPDC-Lock-free-skip-lists-and-Queues.pdf). While there may not be locks they often require interesting atomic instructions and if they are not supported in a language you are using you may end up having to use locks anyway(potentially to implement the atomic instructions) unless you can do some magic akin to the the double-compare and swap mentioned on slide 17&18;
This comment was marked helpful 0 times.


Push: Original: top -> e -> e -> e -> ... Objective: n -> top -> e -> e -> ...
- Make n point to top
- Try to have top point to n. If this fails, restart
This code is different from a spin lock because in locking code, a thread could acquire the lock and then sit for a while (perhaps there's some logic to compute, perhaps it got a pagefault, etc). Now all other threads cannot access the stack.
Here, if a thread freezes before modifying top, this won't halt progress.
This comment was marked helpful 0 times.

The calls to compare_and_swap act to ensure that the stack has not been modified since the thread's entrance into the push or pop functions.
This comment was marked helpful 0 times.

int compare_and_swap (int* reg, int oldval, int newval)
The return value is the old_reg_val.
This comment was marked helpful 0 times.


When thread 0 began its execution of pop, it saw that the current top element of the stack was A.
Then before thread 0 could remove A, thread 1 removed A, added D and added A again.
Now when thread 0 executes compare and swap, it sees that the top of the stack is still A. It assumes that this means the 2nd element in the stack is still B (even though it is now D!), so it sets stack->top to B.
This means D is removed from the stack as well.
This comment was marked helpful 6 times.

Here the main idea is that when Thread 0 recognize A as the top of the stack, and know that the next top is B. Thread 1 pop A, push some other things like D, then push A again. Thread 0 still thinks it is valid in the compare-and-swap operation, therefore it pop two elements which makes stack corruption.
This comment was marked helpful 0 times.

I find this example a bit confusing. In the actual implementation top and new_top are both pointers, but this might not be so clear in this diagram.
In fact, correct me if I'm wrong, but the only time the above example can happen is if thread 1 had called free on A (the pointer) and the allocation of the new "A" pointer gives the same payload address as the just-freed pointer. An extension to that would be that the new pointer wouldn't even need to have "A" as its data, as long as the address of the pointer was that of the just-freed pointer. This is because the CAS signature is
int compare_and_swap (int* reg, int oldval, int newval)
and thus we are only checking for address equivalence (not data).
This comment was marked helpful 0 times.

@markwongsk: In this example, the labels A, B, C, etc. correspond to pointers to nodes. The example is that the node with address A is popped off the stack and maintained as a local variable in Thread 1. Later, thread 1 pushes this node back on the stack. The example is meant to be consistent with the code on the previous slide. As you state, the CAS operation is performed on these pointer values.
Not shown in the example, but another way to create the ABA problem is the case you state. Node A is popped and then deleted by T1. And then later a new node is allocated at the same address A and pushed onto the stack.
This comment was marked helpful 0 times.

@kayvonf okay that cleared things up. Just A,B,C are so generic variable names that I confused them for data values. I guess I should have just trusted typechecking and deduced that type(A) = (void *) given the top = A. Thanks!
This comment was marked helpful 0 times.

More general and easy view of ABA problem: new pointer malloced happens to use the same memory location of removed old pointer, and some memory operations are taken between removing old pointer and malloc new pointer, which makes things bad.
This comment was marked helpful 0 times.


To solve the ABA that this stack pop algorithm introduced, the stack needs some way of uniquely identifying one instance of top field so that it's distinguishing between the top from the time it first read its value from when it performed the swap. Here, the pop_count variable used to ensure that as long as 2^(8*sizeof(int)) pop operations did not occur before this thread finally succeeded in its swap attempt.
This comment was marked helpful 0 times.

I think there's a use-after-free bug here. Another thread might call free() on the value of top before top->next is read. In most cases, you'd survive this because the tag would also change. It wouldn't be valid C, though, and top->next could segfault if free() causes the memory allocator to unmap the page containing top. Wikipedia says that OpenBSD's allocator will do this, and I'd bet that most other allocators do it too.
There are some contexts where this is still useful, though. I used this exact algorithm in kernel code, where you're already abusing C and where you can safely read from a subset of free()'d addresses.
This comes up a lot with lockfree data structures. AFAIK, dealing with it involves some form of garbage collection. In particular, the solutions that I know of involve hazard pointers or reference counting. This paper includes a summary of approaches:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.140.4693&rep=rep1&type=pdf
In this case, the easiest way that I can think of would be to keep a reference count adjacent to &s->top (on the opposite side of pop_count). When popping, read s->top and the reference count atomically as a double word. Then increment the refcount to get a new double word value and do a cmpxchg loop to load the new double word into s. If you detected a refcount > 0, then add top to a set of Nodes to not be truly freed until the refcount reaches 0 again. If, as in this case, the stack doesn't do malloc/free of Nodes internally, then you need support from your memory allocator. Which is a bummer.
This issue has stopped me every time I've tried to write more complicated lockfree algorithms, and it's the motivation for the project that I'm thinking about.
This comment was marked helpful 3 times.

Actually, if you do this, then I think you don't actually need the atomic read, and I think you no longer need pop_count. It would be instructive to prove that.
Here's the thing: how do you actually represent a set of not-to-be-freed nodes? You want something that's lock free (otherwise why bother?), surely something that's less complicated than this stack, and (probably) something that can grow dynamically. One solution that I can think of involves... a lock-free stack, dawg. Like a kernel, an allocator can use the algorithm on this slide safely because it knows exactly which pages are mapped.
This comment was marked helpful 0 times.

EDIT: The slide has been fixed so the 5th argument to double_compare_and_swap is: pop_count. Previously it was s->pop_count. [You may want to refresh the page.]
This comment was marked helpful 0 times.

Also, pop_count should probably be an unsigned integer, since overflow of a signed int is undefined. As is, it's more severe a problem than just wrap around.
This comment was marked helpful 0 times.


Not discussed in lecture, but we can use compare-and-swap to insert into a linked list without locks like we did with the stack. Call the node that will be before the new node after insertion, A. When we find the location we want to insert the new node, we use compare and swap to check that A hasn't been modified before setting A->next to the new node.
In this code's example, we don't have to worry about the ABA problem because when you insert a new node, you are creating a new node (new memory location). The CAS operation will therefore know if the list has been modified no matter what.
This comment was marked helpful 1 times.


It's interesting that the fine-grained locking implementation for the linked list only performed better than coarse-grained locking when the number of threads was between 8 and 16. The paper attributed this to the overhead for the locks protecting the data structure, where $O(n)$ locks have to be acquired and released for fine-grained versus $O(1)$ locks for coarse.
This comment was marked helpful 1 times.

Lock-free implementation can not eliminate contention, so the key point for performance improvement is getting rid of overhead in lock style implementation, such as extra acquire and release lock when there is no contention.
This comment was marked helpful 0 times.

Although lock-free implementation avoid lock usage, it restricted the optimization by memory relaxation. Therefore it may not reduce latency as much as we expected.
This comment was marked helpful 0 times.


When we do not have a sequentially consistent memory system, we frequently need to make use of memory fences. Tools such as CheckFence help in automated verification of memory fences. This tool discovered a bug in this code that was 'formally verified,' underscoring the difficulty of ensuring correctness.
This comment was marked helpful 0 times.


The memsql blog post is pretty interesting. It points out that while lock-free data structures guarantee progress, they may not always be the most efficient in practice. They found that with a naive lock-free implementation of a stack, it performed roughly the same as a stack protected by a mutex. After augmenting the code to sleep after a compare-and-swap failed, it increased throughput by 7 times. And after changing the mutex to a spin-lock with a sleep, they found the lock implementation performed even better than that.
This comment was marked helpful 0 times.







There may be the case that the first value = 0, the second = 10.
Thread 1 holds 3, thread 2 holds 5. They both intend to insert.
The list thread 1 observes can be 0->3->10
The list thread 2 observes can be 0->5->10
This comment was marked helpful 0 times.
More specifically, thread 1 enters the conditional in the while loop, runs the 'prev->next = n' and the 0 node points to 3. Then thread 2 also enters the conditional and the 0 node points to 5. Then both the 3 and 5 nodes point to 10, resulting in:
0 -> 5 -> 10
_____3 -> 10
This comment was marked helpful 0 times.