

Busy waiting is bad because processor that could be used to execute a different task is wasted on useless activity. The overall throughput of system decreases.
This comment was marked helpful 0 times.

If busy waiting is absolutely necessary, one thing you can do so there is not as much useless activity is to check the while condition and then put the thread to sleep() and repeat this cycle. The thread will therefore be sleeping most of the time and not waste CPU resources.
This comment was marked helpful 0 times.

I would argue that sleeping is not the right thing to do here. The other thread which runs when the busy-wait thread sleep()s will probably set the condition to be true, but now the thread which needed the condition is still stuck sleeping, which is bad.
Probably the better thing to do is pthread_yield().
This comment was marked helpful 0 times.

Recap of locking covered in 15-213:
(1) Mutex: mutex offers exclusive, non-recursive execution.
(2) Condition variable: condvar enables a thread to wait until certain event happens.
(3) Semaphore: semaphore controls access to a number of units of resources.
This comment was marked helpful 0 times.

Busy waiting is not necessarily bad. If there's no other work the waiting thread can be doing while it waits and the processor can accommodate the waiting thread without taxing the performance of other threads (i.e. there are free execution contexts,) busy waiting ensures that the instant the blocking condition becomes true the blocked thread will progress. There may be overhead in putting a blocked thread to sleep and waking it up, but not in busy waiting.
This comment was marked helpful 0 times.

@Dave, but at the same time it would be using more power than if it was not consistently spinning while we wait. Though your point still stands from a performance standpoint, from an energy standpoint doing nothing would be better.
This comment was marked helpful 0 times.

@Dave, also if there is multiple tasks waiting on a resource such as a lock, we might want some tasks that have higher priority to run first. By putting all tasks waiting on a resource to sleep, we can evaluate and choose which one to run first.
This comment was marked helpful 0 times.

I also agree with @Dave that busy waiting, or spinning, is not necessarily bad. Spinlocks prevent context switch delays, and are efficient if the thread does not spin for a long time. Apparently, these are often used inside kernels, according to http://en.wikipedia.org/wiki/Spinlock. If someone wants to elaborate on their usage in kernels, that would be great!
This comment was marked helpful 0 times.

Actually this article http://www.linuxjournal.com/article/5833 seems like a good one if anyone is interested in uses of spinlocks in kernels.
This comment was marked helpful 0 times.

system level busy wait is bad on single core machines. If a thread is waiting for a lock held by another thread, it is guarantee not to make any progress while busy waiting since it's using the only core and the other thread won't be able to make any progress(and release the lock). In that case it's almost always better to context switch.
This comment was marked helpful 0 times.

On single-core machines, spinning is basically never what you do. That said, it's supposedly fairly common on multi-core machines. If your critical section is sufficiently short, then it'll take much longer to context switch than to just wait for the other thread to finish, so spinning is a reasonable thing to do.
This comment was marked helpful 0 times.

Busy-waiting is a technique in which a process repeatedly checks to see if a condition is true, such as checking to see if a lock is available. Another way to use it is to cause some time delay, such as how the sleep() function is used sometimes on systems that lacked the sleep() function specifically. However, processor speeds vary a lot from computer to computer. Processor speeds are also dynamically adjusted to the workload of their system, so using busy-waiting as a time delay technique is not a very good idea as then the code won't be consistent across different machines.
This comment was marked helpful 0 times.

Busy waiting is bad since it will waste resources that others could have possibly used.
This comment was marked helpful 0 times.

Busy waiting, while it does have its own advantages, doesn't seem like the method that would be preferred in many cases, since the process is forced to keep on checking while not doing any other potential work. Although doing something else and coming back to check could be costly in some cases, I don't really see why busy waiting would be used except for that reason.
This comment was marked helpful 0 times.


There are specific operations that are used to signal whether or not a condition has been met when working with phtreads/processes.
In shell lab, we used sigsuspend, along with a mask that contained the signals we didn't want to wait on (ie the signals that should awaken the process). So, if we had a job running in the foreground (ie the parent process (the shell) is waiting on a child process (the job) to terminate/stop), we would wait for the job to terminate/stop, while maintaining the ability to reap other terminated/stopped processes.
With pthreads, a similar operation would be pthread_cond_wait. This can be used along with pthread_mutex_lock to block an operation until a condition was met. This was the approach that was used in implementing the thread-safe worker queue that we used in the elastic web server. There are two aspects that make this implementation tricky:
- We should use a lock on the data structure (a vector; STL has no built-in synchronization primitives) whenever we are adding/removing jobs. These locks should be set at the beginning of the calls to get_work/put_work and released at the end.
- However, if the work queue is empty, then calling the
get_workoperation would cause the code to deadlock (if we only used locks), since theget_workoperation needs to check whether the queue is empty. It will not be able to proceed and will wait until a put_work operation replenishes the queue. - Unfortunately, since the get_work operation has acquired the lock, there is no way for the put_work operation to acquire the lock. Hence, we are in a state of deadlock.
In order for this to work, in the case where get_work is called on an empty queue
In the code for get_work, we use the pthread_cond_wait operation, which releases the lock and blocks the thread, until a signal is received from a call to pthread_cond_signal from a different thread. On receiving the signal, the blocked thread will awaken, reacquire the lock and will check the loop condition again; it will break out of the loop when the condition fails.
Crucially, the condition needs to be checked while the thread has ownership of the lock.
This comment was marked helpful 2 times.

When the execution resources are scarce, blocking is better than busy waiting. But in other conditions, it is not necessarily true
This comment was marked helpful 0 times.


Blocking is not always necessary. In applications that do not require outstanding performance or there not not many CPU-intensive applications running at the same time, busy waiting could be used.
This comment was marked helpful 0 times.

A trade-off between the cost of thread switching overhead and wasting cpu cycles. I think the decision depends on the waiting time.
This comment was marked helpful 0 times.

So, after doing some research, it seems that OSSpinLockLock does not use pthread_spin_lock, apparently they did their own spin-locking implementation:
Here are the functions: http://www.opensource.apple.com/source/Libc/Libc-825.40.1/darwin/SpinlocksLoadStoreEx.c
And here some macros they use to do atomic operations (referenced in OSSpinLockLock): http://www.opensource.apple.com/source/Libc/Libc-825.40.1/arm/sys/OSAtomic.h
Oh and it was cool finding Carnegie Mellon copyrights as comments while looking at some files :-)
This comment was marked helpful 0 times.

The source for pthread_spin_lock looks relatively simple. The comment explains the code pretty well, one thing that I thought was interesting was the nested while loops. I believe that this is doing test-and-test-and-set.
The source pthread_mutex_lock was much longer, with many different options. As far as I can tell, the basic lock implementation is in lowlevellock.h, where we have a test and set followed by a lll_futex_wait. There is no test-and-test-and-set here, presumably because we're going to wait for some significant amount of time anyway, so there is no danger of spamming the bus with test-and-sets.
One thing which struck me as interesting was how the spinlock implementation is so much shorter than the mutex implementation. I wonder if this is because:
- Spinlocks are just that much simpler? OR
- There are much more options for mutexes because it is seen as better for most general cases, and expected to be used more often? OR
- Something else entirely?
This comment was marked helpful 0 times.

@eatnow: it's because spinlocks are much, much simpler. Asking the OS or threading library to deschedule you in a way that doesn't create obscure race conditions is not a simple operation, and mutexes often have to do extra work on top of that to ensure some kind of request fairness. Spinlocks are just a while loop (or two, as you pointed out).
This comment was marked helpful 0 times.


Just to make sure I understand how this works. Suppose mem[addr] = 0. This means that the lock is free. So thread A executes the test-and-set instruction and now R0 = 0 but mem[addr] = 1. The compare line is then executed, and R0 = 0, so we do not try to lock again. Note that in this case, if execution is stopped right before the compare line and thread B tries to acquire the lock by doing a test-and-set, the following compare line will cause thread B to branch and try again because R0 won't be 0 (since mem[addr] was previously set to 1 by thread A).
This comment was marked helpful 0 times.

@yrkumar, yea sounds right to me.
This comment was marked helpful 0 times.

Does test and set return the old value of the memory location?
This comment was marked helpful 0 times.

@shabnam I believe that's the usual implementation. That way you have a way to determine whether or not your update went through. Note that if the value at the memory location isn't equal to the value you're testing again, the set doesn't happen.
This comment was marked helpful 0 times.
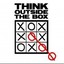
Just to make sure, (relating to cache coherence), every time the processor issues the ts instruction, will it always shout "write x" or would it only shout if mem[addr] = 0 and it's going to write 1 to it?
edit: oops, answered my own question. They will shout write x
This comment was marked helpful 0 times.

@selena731, a test and set instruction indicates an intention to read and possibly write afterwards so the processor will issue a BusRdX causing the other cache which has the lock to invalidate the line in the cache. This is exactly the problem described in exam 1.
This comment was marked helpful 0 times.


This large amount of invalidation is the motivation behind the idea of "test and test and set". If the locked out processors merely attempted to BusRd, not BusRdX, then there would be significantly less interconnect traffic from coherence issues.
This comment was marked helpful 0 times.

In test and set all the threads first try to read a shared variable and then write to it. Hence, while loading that variable we broadcast a BusRdX.
Here in this case proc 1 invalidates every one's cache, reads the test variable and since it passes it holds the lock. During this phase proc 2 and proc 3 also try to get this lock and try in a loop and hence for each try we have p-1 invalidations happening, this also takes the cache line away from proc 1 and hence when it tries to do the set to 0, it has to load the variable into memory again and p-1 invalidations happen.
To reduce invalidation traffic, test and test and set is used.
This comment was marked helpful 0 times.

Is there a reason why 'test-and-set' is implemented as a straightaway BusRdX? I was confused for a long time until I realized that test and set is not a 'test' (BusRd) followed by a set (BusRdx).
This comment was marked helpful 0 times.

@RICEric22, I'm not quite sure, but I would say because you want test and set to be atomic and having two different bus requests could make that more difficult. Also, when you are reading for the test, you are doing so with the intent to write, so that could be another reason why you have a BusRdx.
This comment was marked helpful 0 times.

@RICEric22: it's because of what @ycp said; test-and-set consists of a read followed by an optional write, with the guarantee that nobody else can have that address in the modified state between the read and write. The only way to ensure that this occurs is to get exclusive access to the line up-front, which means a BusRdX.
This comment was marked helpful 0 times.


Does anybody know why there are the dips? As in, it doesn't always increase.
This comment was marked helpful 1 times.

@selena731, if I was to venture a guess, it would be because when you have different number of processors the way that access to the bus is handled changes in a way that is either better or worse for the program that is graphed here. I would also guess that this would change a lot if you simply ran the program again - the dips might occur in different places. In general, it's just more important to note the direct relationship between processors and time to acquire a lock.
This comment was marked helpful 0 times.

My understanding of why the time increases with the number of processors is that when the processor that holds the lock needs to release it (by gaining access to the bus), all the other processors are stupidly taking turns invalidating and gaining exclusive access, thus causing massive amounts of bus traffic. As a result, the processor that actually needs it has to wait for the arbiter to grant it access; this time increases with the number of processors.
This comment was marked helpful 0 times.

There is a great paper from MIT CSAIL talking about the spin lock performance for linux scalability: An Analysis of Linux Scalability to Many Cores. It's a very good paper and talks about the same thing in the lecture. But you can see many live examples of its impact on linux scalability.
This comment was marked helpful 1 times.

@selena731 Another possible reason is that the different topology might be used for different number of processors
This comment was marked helpful 0 times.


To address the issue about provision of fairness, it seems like here, the order in which processors get the lock is dependent on which processor is successfully able to broadcast a BusRdx ==> The fairness is dependent on the fairness of the bus arbiter which decides who can use the bus.
This comment was marked helpful 0 times.


Why is the while (*lock != 0); used here? Wouldn't the code be the same if the while and if were replaced with a short circuit and such as if (*lock == 0 && test_and_set(*lock) == 0) or just two nested if statements?
This comment was marked helpful 0 times.

@sss: Because we don't want to call test and set ( which actually modifies the memory location ) until we actually think thats the case. Till then we spin and wait to see if its worth calling test and set and only then call it.
This comment was marked helpful 0 times.

I think a short-circuit would do the same thing there though. We're spinning anyway in the while(1), so if you keep checking on the condition if lock == 0 && test_and_set(*lock) == 0, if the lock value were set to 1 then it would short-circuit and you wouldn't actually perform the test_and_set in that case either. I'm not sure what the answer to the original query is though, except I guess it's one way of doing it.
This comment was marked helpful 0 times.

I agree with @arsenal, using the if (*lock == 0 && test_and_set(*lock) == 0) condition would behave the same way, because the test_and_set will still only get called if the lock is 0.
I can't think of any scenarios where they would perform differently, I believe these are just two different ways of implementing the test_and_test_and_set lock.
This comment was marked helpful 0 times.

@everyone: Your understanding is correct.
This comment was marked helpful 1 times.
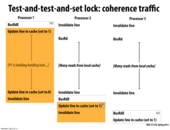

The difference between test-and-set and test-and-test-and-set is in the latter we first do a read, while (lock!=0) and then only if this passes we do the test and set. Hence, the only invalidations that happen is when proc 1 sets the lock variable to 1 and then to 0 when its done. This is because as soon as proc 1 gets the lock proc 2 and proc 3 just keep spinning on while (lock!=0) and since this is just a BusRd they do not trigger cache invalidations. Another advantage is this does not snatch the line away from proc 1 and hence proc 1 does not have to load the lock variable back into memory before setting it to 0 at the end.
This comment was marked helpful 1 times.

I'll also add that after the first BusRd, there isn't any more traffic on the bus until the lock is released (unless there is a directory based cache structure). But then, when the lock is released, all other processors will have the lock invalidated, and will have to read the new one (which is set by whichever processor happens to be granted bus access first).
This comment was marked helpful 1 times.

Isn't there a BusUpg before 'Update line in cache' in processor one?
This comment was marked helpful 0 times.

@Yuyang. Yes, you are correct. It's not shown. It could also be a BusRdX if the line containing the lock happened to be evicted during the critical section.
This comment was marked helpful 0 times.

So it seems this kind of optimization is highly dependent on the implementation of the hardware. Does anyone know how does linux kernel developers deal with the variety of hardwares and protocols used when developing kernel for it to work well on all platforms?
This comment was marked helpful 0 times.


I did not understand why O(P^2) traffic. When test-and-set lock for each processor generates invalidation message, suppose all P processors gets to the test-and-set part, then at most P invalidations. But when the first invalidation occurs(from the first test-and-set), other processor cache would go to I state, for the next test-and-set operation, only one processor cache (in M state) would be invalidated.
This comment was marked helpful 0 times.

@yanzhan2: I think the assumption here is the critical section is long enough, so that all other processors are doing "test". Then all processors waiting for the lock is in the S state. So in each round, O(P) traffic occur and for P rounds there are at most O(P^2) traffic.
This comment was marked helpful 1 times.

Why do we look at P rounds of lock releases? Specifically, on slide 19, one comment by @sbly implies that the $O(P)$ traffic cited is from one round of lock releases.
Of course, assuming we look at P rounds of lock releases makes the two slides consistent, but that makes me wonder why, on slide 19, traffic is not O(P) per lock release (see my comment there).
Also, why look at P rounds in the first place? Because each processor wants the lock and thus must at some point release it?
This comment was marked helpful 0 times.

I think the slide makes the assumption that the lock is contested for by P processors, which is what is shown on slides 12 and 16. It says that if there are O(P) invalidations (which means P rounds, each round has 2 invalidations) then there would be O(P^2) traffic total. Assuming constant/O(1) invalidations, then yes from that one round there would only be O(P) traffic.
This comment was marked helpful 0 times.

@tcz, @LilWaynesFather,the comparison is for one round, so for TTS lock, worst case scenario one release would cause O(p^2) traffic (refer to later slides for explanation), but ticket lock would cause O(p) traffic.
This comment was marked helpful 0 times.

@tcz @yanzhan2 @yetianx @LilWaynesFather
During one lock release the number of invalidations is $O(P)$, and the amount of traffic is $O(P^2)$.
Here the lock is held by a processor p1, the other $P-1$ processors are waiting for the lock. When p1 releases the lock, it will invalidate all the other $P-1$ processor's cache entries (1st invalidation). All the $P-1$ processors, that were waiting for the lock, pass the outer test of the test-and-test-and-set. They are now all trying to get the lock using test-and-set. Each processor will need exclusive access to the cache line in order to be able to run the test-and-set. This means $P-1$ more invalidations must occur, allowing each processor to have exclusive access to the line, while it runs test-and-set. In total we had about $P$ invalidations, so $O(P)$ invalidations. Each invalidation causes $O(P)$ bus traffic (communicating with each of the other processors), giving a total of $O(P^2)$ bus traffic.
This comment was marked helpful 0 times.

@mofarrel, that depends on how you define traffic, if you define snoop based protocol, and traffic is snoop traffic, then it would be fine. Other wise, if you define traffic as messages, then it is not that easy to construct O(p^2).
This comment was marked helpful 0 times.

I think this slide is slightly confusing with its wording. By $O(P)$ invalidations, it meant, $O(P)$ BusRdx were issued. And by $O(P^2)$ traffic, it meant there are worst case $O(P^2)$ occurrences where a processor invalidates its own cache.
This comment was marked helpful 1 times.


In the DMV example, this lock would be analogous to going up to the teller and asking if they are busy. If they are, you leave and come back after X minutes and repeat the process. If they are not you get your turn.
There are multiple problems with this scheme however. From the DMV's perspective, when the teller is free, no one may be there to take their turn so throughput is low. From the user's perspective, if their return to the DMV does not line up exactly with when the teller becomes free, someone else will probably already have claimed the teller, so latency is high and fairness is low.
This comment was marked helpful 2 times.

A similar strategy is used to avoid conflict of sending packages to the wireless network. But in that case, an upper bound of delaying time increases in a exponential way. And the delay time is randomly chosen from [0, upper bound).
Maybe the random number generator is too expensive to use in the lock implement.
This comment was marked helpful 0 times.

@yetianx I don't think that's the case, I think this is just a very simple example. I think randomly choosing a wait time for each processor would be a much better scheme, especially in terms of fairness. That way, locks that keep missing the lock wouldn't be punished; in expectation each processor would get the lock the same amount of times.
This comment was marked helpful 0 times.

It seems as though exponential back-off for waiting is used to improve scalability by reducing busy-waiting. As noted before, it probably wouldn't be practical for critical sections with high contention. Here's an interesting link about scalable locks.
This comment was marked helpful 0 times.

At first it seemed to me like this implementation was pretty useless, since it has the same or worse performance characteristics in most cases as test-and-test-and-set. But then I realized that the type of lock used should depend on what is expected to happen in the program... For example, test-and-set with back-off would probably be better than both test-and-set and test-and-test-and-set in the case where low contention is expected. The latency is the same as test-and-set (better than test-and-test-and-set), there is less traffic and more scalability as in test-and-test-and-set, and the storage is the same. Although this implementation has the drawback of possible extreme unfairness, this is unlikely to happen in the case of low contention, because the process will probably acquire the lock after just a few iterations.
This comment was marked helpful 0 times.

@sbly I don't see how a random number generator would be better than just a constant delay time. In expectation the traffic would be equally high in both cases, but fairness seems like it could only be worse with randomly chosen delays. I agree with @bstan and @jmnash that exponential delays seem like a good scheme to reduce traffic in situations with low contention.
This comment was marked helpful 0 times.

@jhhardin
If the critical section takes a very consistent amount of time, I could think of some (extreme) edge cases where the timing of the constant delay just so happens that a certain worker always asks for it at the wrong time for many iterations in a row. Imagine that the delay is about as long as the critical section computational time but this worker always asks for the lock in roughly the middle of the computational time, and contention is high so timing doesn't change much. Making it random avoids any such odd cases.
This comment was marked helpful 0 times.


In class, we talked about how a ticket lock is analogous to waiting to be served at the DMV. The critical section in this case would be the teller. If tellers simply shouted out every time they were free, then we would have a rush of people, and it would be a mess. Instead, each person takes a ticket with a number on it, and tellers increment the "now serving" sign when they are free. A person gets served only when their ticket number is the same as the "now serving" number. Thus, people are served in the order that they arrived (which corresponds to their ticket numbers), and only one person is served at a time. In code, each "ticket" and the "now serving sign" are integers.
This comment was marked helpful 0 times.

Only one invalidation per lock release, but all the other processors needs to read the new now_serving variable, would that cause traffic? So traffic is O(P) refers to one lock release, or P release?
This comment was marked helpful 0 times.

@yanzhan The O(P) traffic refers to one lock release. There is only one invalidation, but that invalidation is seen by all P processors.
This comment was marked helpful 0 times.

@sbly, thanks, can you also explain why P^2 traffic for test-test-and-set lock 2 slides before?
This comment was marked helpful 0 times.

@yanzhan This is the worst-case scenario. It is possible that after the lock is released, all processors break out of the
while(*lock != 0);
loop before any of them perform the
test_and_set(*lock)
code. In this case, all $P$ processors will execute the
test_and_set(*lock)
which will invalidate the cache for all other $P$ processors. Thus the total traffic is $O(P)*O(P) = O(P^2)$.
This comment was marked helpful 4 times.

@sbly, thanks, it makes sense. But my question is fro all P processors execute test_and_set, after the first one is executed, there should be only one in M state, later P-1 test_and_test does not need to invalidate all P caches, 1 is enough. So I think it is O(P)+O(P) = O(P).
This comment was marked helpful 0 times.

It does need to invalidate all $P$ caches every time. All the cache have a copy of lock. Whenever a processor performs test_and_set(&lock;), it counts as a write (even if a write does not actually happen), so the cache line becomes invalidated and the other processors must retrieve the "updated" copy (though it is actually the same value).
This comment was marked helpful 0 times.

@sbly, thanks, but I think the case is more accurately that each processor would execute test-and-set then enter the while loop, so the traffic is 1+2+..P-1, so O(P^2).
This comment was marked helpful 0 times.

I don't see why there is only one cache invalidation per lock release. During the critical section, all processors should in theory be sharing the lock's line in cache. Say processor 0 writes some value to the now_serving line. It would have to issue a BusRdX. This should invalidate everyone else's cache line, according to the MSI protocol from the consistency lecture. So, I think there would be one invalidation per processor per lock release.
This comment was marked helpful 0 times.

Why might we not use a ticket lock? It seems considerably simpler than other spinlocks and ensures fairness.
This comment was marked helpful 0 times.

If anything, the ticket lock does theoretically limit the number of processors in your system to the range of values that the number holding the ticket can reach.
For example, in an 8 bit ticket count variable, we can maintain a system that has 256 independent cores at maximum.
This comment was marked helpful 0 times.

The main issue is that the system will map elements of the struct to consecutive locations in memory that will most likely be on the same cache line. Thus, whenever a processor acquires a lock (performs an increment on next_ticket), every processor waiting on now_serving will have to invalidate their cache line, leading to higher coherence traffic.
Another possible flaw is that limiting your next_ticket to a b-bit number will only work on a system with up to 2^b processors. For 32-bit there is probably no practical system that will hit this limit for a long time, but its still a concern to scalability
This comment was marked helpful 0 times.

@tcz, one invalidation means exactly the same with what you said. It means one invalidation message send from the processor which releases the lock, like a BusRdX request. So the traffic is O(p), which means P invalidation messages are sent to P processors. I would say it is just the understanding is different, but it means the same thing.
This comment was marked helpful 0 times.

@sbly, what you said is like an update CC protocol, and what I am confused at first is invalidation CC protocol. But the worst case scenario are both O(P^2) for TTS lock.
This comment was marked helpful 0 times.


We could think of this as conceptually similar to a ticket lock (a queue-based system), except that the queue is implemented with a series of binary-valued variables on separate cache lines instead of a single shared integer, reducing the amount of cache invalidation.
This comment was marked helpful 0 times.

An issue with this type of lock is that it has a limit to the number of waiters, P. In the latest Linux kernel (3.15) they combat this limit while maintaining a separate status per waiter by using something called an MCS lock described here. The link has a pretty good description, but essentially, an MCS lock replaces the array in this example with a linked list which allows for an unbounded number of waiters.
This comment was marked helpful 2 times.

An important note is that the starting state for the l->status array would be the first element being 0 and everything else being 1. This way the first to the lock can run and all proceeding lockers wait.
This comment was marked helpful 0 times.

This seems to waste a bit of space, as each cache line only holds a single integer (actually a single bit) just to implement a lock. Luckily, it doesn't seem that this is substantial due to the fact that the number of processors is limited. I believe that this lock still runs into the problem of all the processors spinning on a value while waiting for the unlock of their index, although perhaps this can't be helped if all the processors get to this stage at the same time.
This comment was marked helpful 0 times.


(Kayvon said he was going to change this in class, so I'm going to comment on the version that I currently see)
There was a presentation of atomicIncrement which takes arguments int *x and int y. This implementation attempted to increment by any arbitrary amount, but could be broken by supplying values for y which are alternating negative and positive.
In the meantime, pretend that y is actually "uint", not int. This makes the atomicIncrement code more safe.
This comment was marked helpful 0 times.

x86 offers 8 byte and 16 byte CAS instructions. How does the processor handle these instructions if the bytes they're modifying span cache lines? Does it just not guarantee atomicity? or does it have some scheme of acquiring and hanging onto one cache line while it finishes modifying the second?
This comment was marked helpful 0 times.

This implementation of atomicIncrement may have the same performance issue when the lock is highly contended. I think this function can also be implemented as test-and-atomicIncrement, which is equivalent to test-and-test-and-set.
void testAtomicIncrement(int* x! unsigned int y) {
while (1) {
int xold;
int xnew;
do {
xold = *x;
xnew = xold + y;
} while (*x != xold);
if (atomicCAS(x, xold, xnew) == xold)
return;
}
}
This comment was marked helpful 1 times.

@tchitten: Most datatypes are aligned by their own size, so 8-byte integers would be aligned on a 8-byte boundary, and 16-byte integers would be aligned on a 16-byte boundary. Because cache lines are 64-bytes on most modern processors, both of the above datatypes would fit just fine into a single cache line.
Not too sure what would happen once the size of a datatype exceeds the cache line size, but I imagine atomic operations on it would either require locks or transactional memory.
This comment was marked helpful 0 times.


The problem with this implementation of the barrier is that although it ensures all threads WAIT up to some point, it does not ensure that all threads LEAVE.
If ANY threads are left behind in the while(b->flag == 0) statement (keep in mind, b->flag will actually be one, but they will not have had the chance to evaluate it yet), and ANOTHER barrier is called, the flag will be reset to zero.
Some threads will be stuck on the first barrier, and some threads will be stuck on the second barrier. All threads will be stuck.
This comment was marked helpful 2 times.

An alternative solution is to use a different barrier variable. If a thread hits the second barrier, it would update an independent flag and there wouldn't be a dead lock. Note that the solution on slide 25 uses two flags conceptually by flipping the value of flag.
This comment was marked helpful 0 times.

The exact interleaving of processor steps that would lead to the deadlock would be:
processor 0 reaches barrier 1 and sets b flag to 0, then begins waiting processor 1 reaches barrier 1 and sets b flag to 1 processor 1 does the code in between barriers processor 1 reaches barrier 2 and sets b flag to 0, then begins waiting
Now both processors are waiting for the b flag, but they're waiting at different barriers, so neither barrier will ever reach the threshold of 2 processors to set the b flag to 1.
A possible solution to this would be to somehow force the while condition to be checked every so often, or alternatively we would have no problems if the work between the barriers is expensive/lengthy enough that processor 0 will definitely get a chance to check before processor 1 finishes the work. But this is certainly completely invalid as a general-purpose barrier or as a black box barrier implementation.
This comment was marked helpful 0 times.

I was thinking that another way to solve the problem would be:
Instead of making the last process set b->counter = 0, just set flag = 1, then each process would need to decrease counter by one right after leaving the barrier. Now, the next time we enter the barrier and set flag = 0 again, we are guaranteed that all the processes left the previous barrier.
One drawback of this approach is that we would need to use a lock again; to update the counter, or we can use an atomic add to avoid the lock. But even if we use atomic add, we would be generating interconnect traffic by invalidating the cache line containing the counter.
This comment was marked helpful 0 times.

Just as a refresher, for the line int arrived = ++(b->counter), it is important that the increment operator ++ comes before (b->counter) because that ensures that arrived is set to the same value as b->counter after the increment. If instead we had int arrived = (b->counter)++, then arrived would instead be set to the value of b->counter before the increment, which would result in all processors waiting forever for everyone to arrive at the barrier, even when each processor has already arrived...
This comment was marked helpful 0 times.


In the previous slide, we only keep track of the number of threads that enter into the barrier, which can cause deadlock. One way to solve this is to keep track of two variables, one which denotes the number of threads that have entered, and another that denotes the number of threads that have left. This way threads that enter into the second barrier can wait until all threads have exited the first barrier.
This comment was marked helpful 0 times.

Note the lock on line 15 and 17 is actually b->lock. A key point is that the while (b->leave_counter != P) relinquishes the lock before it does any checking and then is able to get the lock back before it sets the flag to 0. This ensures that every other thread is not within the process of updating leave_counter and we have guaranteed every thread has left.
This comment was marked helpful 0 times.

Another way of looking at these barrier implementations is that the flag exists as the actual "barrier" that stalls processors until every processor has reached that point. What this solution and the one of the following slide presents are ways of controlling this flag so that it has the desired behavior.
This comment was marked helpful 0 times.

Line 21 should be int arrived = ++(b->arrive_counter).
This comment was marked helpful 0 times.


The nice idea of this implementation is that no thread can set the b->flag twice until other threads leaving the previous round. It's not based on the b->counter, so prevent one thread from modifying the b->flag twice.
This comment was marked helpful 0 times.

This works by effectively assigning each barrier location in the code a different target flag value, alternating between 0 and 1. Then, the flag variable will not match the target value until everybody has left the old barrier location. When all locations have the same target value, as in slide 23, then there is no distinguishing which barrier a processor is waiting at.
A more obvious and equivalent solution is to simply assign each location an incrementally increasing target value, such as barrier 0, barrier 1, barrier 2, etc. Then, when the last thread reaches barrier location x, it updates the flag to x. However, the solution in the slide is, I think, more elegant.
This comment was marked helpful 3 times.

This is so much better than the leaving counter!
This comment was marked helpful 0 times.


Can someone explain how latency is O(P).
This comment was marked helpful 0 times.

@shabnam I think it's because all the processors (P of them) have to each lock, add one to the count, and unlock. And this sequence can only be executing by a single processor. So this means that there's serialized access to a single variable. Which equates to a latency that grows linearly with the number of processors.
This comment was marked helpful 0 times.
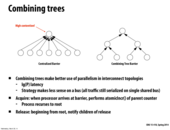

Is there any downside to using this tree combining strategy on a single shared bus, or is the just no real benefit?
This comment was marked helpful 0 times.

@cardiff I think the latter. If using a flat topology then there's going to be O(P) traffic either way.
This comment was marked helpful 0 times.

On a single shared bus, even though we use a tree based combining strategy, we can not parallelize the operations in different subtrees because of the contention of the bus, so there is not benefit using this strategy. It's even worse since the tree based combining strategy is much more complicated.
This comment was marked helpful 0 times.


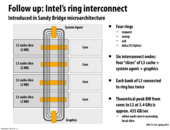








It's interesting to note that each core's L3 is connected to the ring (which is unidirectional) in two places. This is primarily to reduce the number of hops from one core to any other core, which helps to reduce latency.
If the caches were only connected to the ring in one place, then getting a message from core #4 to core #3 could potentially require going though the graphics node, the system agent node, and cores #1 and #2 before reaching core #3. If the caches are connected to both sides of the ring, then core #4 can send a message to core #3 in just one hop.
This comment was marked helpful 3 times.
Oh that's cool! I was wondering why they would ever use a ring (precisely for that reason)
This comment was marked helpful 0 times.
Well, the other reason to use a ring is that the bus circuitry and implementing logic only has be able to send messages in one direction.
I think it is very likely that the intel designers place some flip-flops at each yellow rectangle, so that on each ring-clock edge, the values in each flip-flop for one yellow rectangle get forwarded to the next rectangle. If they had to implement bi-directionality, I suppose they would need twice the hardware, or some sort of scheduling system so that they could coordinate using a wire for two directions.
This comment was marked helpful 0 times.