

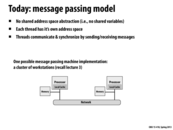
Here we are reminded that the message-passing model, unlike the data parallel and shared memory models, has no shared address space. In these two models, every process had access to the entire grid, and only computed the portion to which it is assigned. In a message passing model, however, each separate process has its own address space, and thus has full ownership of (that is, can load/store only to) its portion of the grid.
This comment was marked helpful 0 times.


In the message passing model, each node has its own address space, so there is no single block that all processors can read and write to. Therefore the processors need to issue a receive (and a send not shown) in order to communicate.
This comment was marked helpful 0 times.

Question: Assuming that each row has N items, is there a reason we allocate N+2 cells for each ghost row in the code shown? Or are we just working under the assumption that each row has N+2 items?
This comment was marked helpful 0 times.

@placebo. It is the latter case. The gird itself is (N+2)*(N+2). You can find the problem description in lecture 4, slide 21.
This comment was marked helpful 0 times.

In a shared address space model, thread 2 would simply issue loads for the last row from thread 1 and the first row from thread 3 directly from the hardware level. In the message passing model, it has to request those two rows of data through message passing.
This comment was marked helpful 0 times.


Line 6: Each thread now only allocates an array corresponding to the size of its block, plus two extra rows (to copy data from other blocks that it needs). Since the threads do not share memory now, we don't need to worry about ensuring mutually exclusive array modifications.
This comment was marked helpful 1 times.

All the threads other than thread 0 send their computation result to thread 0 (line 25b). Thread 0 receives (25f) and sums up all the floating numbers (25g) it gets from every other thread. Depending on the value, thread 0 tells every other thread whether the computation is done or not. According to what was sent from thread 0, computation will either stop or continue.
This comment was marked helpful 0 times.


Mutual exclusion is inherent from this model. There is no way for two processors to write to any shared memory.
This comment was marked helpful 0 times.

Question:
What happens when thread A and thread B both send conflicting information to thread C? Say thread A says x = 3 and thread B says x = 4. What is thread C going to think x equals? What type of synchronization (if any) is needed for cases like this?
This comment was marked helpful 0 times.

@nslobody That would probably depend on the program. If thread C only calls receive once, then this would be a race condition and depends on if your program views that as the correct state or not, perhaps either of the cases are valid. If there's a reason for thread C to have to call receive more than once, then perhaps there's a reason for the volatility of x. In that case I would think that you would need to provide more synchronization which also depends on your program. Perhaps have thread C indicate that it's ready to receive a value for x from one thread before allowing another to provide a value for x.
This comment was marked helpful 0 times.

@nslobody: It's not "conflicting information" from the programming model's standpoint. The program simply sends thread C two messages.
- Thread A sends C a message (message contents are 3)
- Thread B sends C a message (message contents are 4)
Thread C will explicitly receive those messages and store their contents somewhere in its own address space as determined by the program. Below, I wrote code that stores the message's contents in local variable x. The content of the first message is saved to x. Then, the content of the second message is saved to x. After the two messages are received by thread C, x contains the value 4.
int x;
receive(FROM_A, &x, sizeof(int));
receive(FROM_B, &x, sizeof(int));
Note the key point here is that a message is simply a message, interpreted and stored by the receiving thread in whatever manner the programmer specifies. Thread C could just as easily be written to handle receipt of the same two messages using the following logic:
int x, y;
receive(FROM_A, &x, sizeof(int));
receive(FROM_B, &y, sizeof(int));
A thread can interpret the contents of a message however it wants. Imagine the program is changed so that the messages now contain two integers, and you coded up the simple function below that uses the value of the first integer to designate where to store the second integer in the receiving thread's address space.
void myReceiveFunction(int source, int& x, int& y) {
int msg[2];
receive(source, msg, 2 * sizeof(int));
if (msg[0] == 0)
x = msg[1];
else
y = msg[1];
}
Then, code for the receiving thread C might look like this:
int x, y;
myReceiveFunction(FROM_A, x, y);
myReceiveFunction(FROM_B, x, y);
This comment was marked helpful 0 times.


If all processors are blocking to send, and none are receiving, then it deadlocks.
This comment was marked helpful 0 times.


This code will deadlock for blocking send/receive. One solution is to send/receive to the thread under you, and then send/receive to the thread above you. In this way, thread 0 will receive first since it has nothing to send, and the receives will cascade upwards, and then cascade back downwards, for the second round of message passing since thread N-1 has nothing to send and thus will receive first. However, this ends up making all communications sequential.
A far better solution is for even rows to send first while odd rows receive first so we can communicate in parallel.
This comment was marked helpful 0 times.

What might an optimal message passing algorithm be in a two or three dimensional system?
A naive solution, an extension of that above, can run in time linear with the maximum dimension, by sending towards one corner, receiving those, sending towards the opposite corner and then receiving those.
This comment was marked helpful 0 times.

Just to add an example of deadlock situation: If every processors send a row to the neighboring processor (blocking send), then every processors would have to wait for the blocking send to return. However, since every processors are doing blocking sending and wait, no thread can perform blocking receive. Thus, the program deadlocks as every processors are waiting for their blocking send to return.
This comment was marked helpful 1 times.

@FooManchu: For 2D case i wonder if a red-black pattern as in the solver example work? All red cells will send and all black ones will receive. This way all the blocking sends of the red cells will be acknowledged by the receive call of black ones and then the roles can be reversed where all black cells send and all red ones receive.
One thing we might have to take care is that if the sequence of send call from red cells is:
send(right)
send(left)
send(top)
send(bottom)
Then the receive calls from black cells should be in the following order:
receive(left)
receive(right)
receive(bottom)
receive(top)
If the order of receive is first right followed by left, then it will result in a deadlock.
This comment was marked helpful 0 times.

@Mayank I think your proposed solution is increasing the total amount of communications by a huge amount, and the overhead of such communications will offset any benefits gained.
This comment was marked helpful 0 times.


@Question I'm a little unsure why an "asynchronous blocking" send is blocking. From the point of view of the program, isn't it non-blocking? It seems that the only difference between this and the "non-blocking async" on the next slide is that this send is free to reuse the send buffer immediately after send() terminates. Couldn't you argue that if the system offered a sent message queue that could be arbitrarily large, then they behave the same way? (the version on this slide would also be easier to reason about)
This comment was marked helpful 0 times.

@kfc9001: your understanding is essentially correct. With a finite queue implementation, the call may block the caller if the internal message library buffer is full. This cannot happen with non-blocking async send, since the buffer space is provided by the caller.
I agree it's not the best name (but this is convention).
Typically blocking (synchronous) and non-blocking async are the only two variants we care to think about.
This comment was marked helpful 0 times.


As a note mentioned in class, this assumes that all messages get to their recipient eventually, which is a problem you deal with in 440. Additionally, while it is possible to overflow the sending buffer it shouldn't be something we should worry about either.
This comment was marked helpful 0 times.

Question: Why might a programmer choose to use an asynchronous (non-blocking) send, as opposed to a blocking send?
This comment was marked helpful 0 times.

If the programmer knows that the value being sent will not be modified before the receiver receives it, he might prefer non-blocking messages because the sender can continue its execution immediately after sending. As was mentioned in class, this is presumably how purely functional languages work under the hood, since they do not allow assignment (variables aren't mutable).
This comment was marked helpful 0 times.

Non-blocking sends generally perform better in terms of performance than blocking sends, since network delays are arbitrary and, as nslobody mentioned, non-blocking send allows the program to continue is execution. On the other hand, blocking sends are much better synchronization primitives than non-blocking sends. They are commonly used as rendezvous points and as ordering mechanisms. These features are very hard to implement (if not impossible in some cases) using non-blocking sends. For example in a data-parallel programming model, non-blocking send can perform much better, since all data are independent and ordering does not generally matter. Transactions and logging on the other hand are good examples where blocking sends are more useful, since the users are more concern about ordering than total throughput.
One personal experience I have is to never use non-blocking sends to solve deadlock problems caused by blocking sends. It might sound tempting at first, but if blocking sends are causing deadlock, this generally implies an underlying design inconsistency. By using a non-blocking send in such case might seem to solve the problem at first, but soon enough more and more synchronization bugs will start surfacing.
This comment was marked helpful 0 times.

Question: Is sendprobe(h1) blocking? Or do we need to keep polling? In other words, how do we handle cases when sendprobe indicates that the message has not been sent? What about recvprobe?
This comment was marked helpful 0 times.

@Mayank: Yes, they are intended to be non-blocking in the slide. The calling thread would need to keep polling if it wanted to wait until the send or receive had completed. Of course, most messaging APIs provide a blocking probe variant as well. In MPI MPI_Probe() is the blocking variant, and MPI_Iprobe() is the non-blocking variant.
This comment was marked helpful 0 times.


A comment on the phrase: "It scales" - you don't need to complicate your algorithm in order to completely parallelize computation into millions of separate parts. In reality you won't really be scaling infinitely. You really only need to break up your code to scale to the number of processors you have (or expect to have in your machines for the foreseeable future).
This comment was marked helpful 1 times.


In my view, another discussion on the workload balance on SIMD is also necessary. Because they run instructions lockstep, the running time is decided by the slowest one, while others have to wait for it. So it is better for us to schedule the similar-length ones together to use SIMD. But it may increase the cost in pre-process or memory loading for such optimization.
This comment was marked helpful 0 times.

Your discussion also reminds me of branch prediction. Remember if the instructions run on a SIMD unit has if...else statements, both branches will be calculated by all SIMD units, and the result of the invalid ones will be discarded. Although branch prediction is an important area studied by many, it's still not perfect. Hence it might also help if the programmer keeps Amdahl's law in mind while coding and make the program easier to be split into balanced parts (e.g. reduce the number of branches so SIMD processing can be more efficient).
This comment was marked helpful 0 times.


As mentioned in lecture, static assignment is perfect when workloads have predictable cost. There is certainty before the work actually starts, that the work loads will remain balanced. The cores that are assigned work will all finish about the same time without any work needing to be reallocated after the work starts.
Note: Predictable doesn't mean that you know exactly how long each sub-problem will take. For example, for the square-root problem in homework 1, it was random how long finding the square root of a number would take. But in expectation, the work was split up evenly so static assignment was appropriate.
This comment was marked helpful 0 times.

Question: Here I claim that the static assignment has "essentially zero" runtime overhead. What did it mean by this? When I say overhead, what is the baseline that I am comparing to? In slide 26 introduce the idea of dynamic assignment. What is the "overhead" of performing a dynamic assignment of work to worker threads in that example?
This comment was marked helpful 0 times.

I believe that the baseline we are comparing to here is the sequential version of the algorithm. In the sequential version, every task is picked up when the previous one is done, and hence the processor is always doing useful works. In the static assignment version, each processor are assigned a static amount of work. In other words, for each processor, it is essentially performing the sequential algorithm, which, as we just mentioned, has (nearly) no overhead. And therefore, the only overhead involved in the static assignment version is the work spent for setting up a multi-thread environment to run the code and the time spent for exchanging information between threads. And this overhead can be ignored if the tasks assigned to each thread are large enough. In the dynamic assignment version, the overhead could be two things: (1) the time spent for the function calls to $lock$ and $unlock$; (2) the time spent for waiting the lock. For the first kind of overhead, it depends on implementation of the lock. If the lock contains several system calls, we may need to trap into kernel mode multiple times, which is costly. For the second kind of overhead, since at any given time, there can be only one thread inside the critical section, other threads that want to increment the counter can do nothing but wait for the lock, which is also costly.
This comment was marked helpful 2 times.

In a reasonable implementation, a mutex lock/unlock takes ~17ns. From Latency Numbers Every Programmer Should Know.
This comment was marked helpful 2 times.


In program 1 (Mandelbrot) of Assignment 1, the cost of each piece of work (each row) was known ahead of time. Because of this, a static assignment was appropriate, and we could predict the performance of a static assignment based on which rows of the image were assigned to each processor.
(Note that my Mandelbrot example doesn't match the example illustrated on this slide, since not all rows in the Mandelbrot image had the same cost to compute.)
This comment was marked helpful 0 times.

@mschervi: You are on the right track, but are you sure you knew the cost of a row ahead of time in Assignment 1? Weren't some rows significantly more expensive than others, and it took rendering the picture to figure that out? I suppose that if you ran the program once, you'd know the costs, and then you could use that information if you ran the program again on the same input. (But that's not particularly helpful, since you're using the answer to compute the answer!)
A static assignment was appropriate in Assignment 1, program 1, but I don't believe you got by with static assignment because you knew the cost of each row up front. Care to clarify? (Hint: consider example 3 on the next slide.)
This comment was marked helpful 0 times.

It wasn't that we knew the cost of each piece of work, but that we knew the distribution of work. It was necessary to assign work such that the jobs (rows) given to each core weren't biased towards a particular part of the total work distribution (the center).
It seems like a very powerful strategy, as it's probably very realistic to know something about how work is distributed over a set of jobs.
This comment was marked helpful 2 times.


When predicting, we should consider both the work quantity on each core and the cost of each piece of work. The workload may not be evenly distributed.(like problem 1 in Assignment 1) An analogy is as follows: When we statically assign a branch of clothes into 4 laundries, the best approach is not making each laundry have the same amount of clothes. The time difference of each clothes also counts. For example, cleaning one feather jacket will take longer time than a T-shirt even though the procedure is the same(remind the SIMD abstraction). We can treat this as the "density" of workload in some way. In programmer's point of view, it is common to ignore the workload "density" when statically allocating.
This comment was marked helpful 0 times.


Semi-static assignment is a hybrid of static and dynamic assignment in that it has properties of both. First, all the work is assigned statically, but after a some amount of time, the workload can be re-evaluated and reallocated. This is different from straight-up dynamic allocation because there is some initial allocation that gets updated. Dynamic allocation, by contrast, has threads call for work when they have nothing to do.
This comment was marked helpful 0 times.

We can view semi-static assignment as if there is a sequence of static assignments in the program. Instead of adopting the same strategy for each phase, we "learn" from the previous results to make better static assignments in future rounds.
This comment was marked helpful 2 times.

Semi-static assignment attempts to take the good portions of both static and dynamic assignments by periodically adjusting the static assignment based on past results. Ideally, this would have less overhead than a pure dynamic assignment and a more balanced work distribution as a pure static assignment. However, it is up to the programmer to decide how periodically the static assignment is adjusted. If the assignment is adjusted too frequently the overhead increases and if it is adjusted too infrequently the work distribution becomes unbalanced.
This comment was marked helpful 0 times.


Each task is simply to check whether x[i] is prime or not. A thread gets assigned a piece of work by taking the number need to be check at index i which is indicated by the counter. This ensures that every number is checked once and only once due to atomic increment.
This comment was marked helpful 0 times.

By drawing new numbers whenever they have finished their work, all threads are kept busy, much as if they were pulling jobs off of a queue.
This comment was marked helpful 0 times.
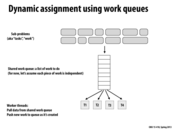

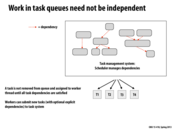
A dynamic assignment is one determined at runtime in order to achieve an even distribution of load. This is applicable when the cost of the tasks is unpredictable, and therefore cannot be evenly distributed beforehand. In this model, dynamic assignment is implemented through a shared work queue. Rather than dividing the tasks amongst the threads initially, there is a queue which lists all of the work to be done. Each thread can then pull a task from the queue to perform when it has finished the previous task. In this way threads do not need to wait for others to terminate once they have finished their work, they can simply pull another task to work on.
This comment was marked helpful 0 times.


If the numbers are big enough for you to bother parallelizing it, the synchronization cost probably doesn't matter.
This comment was marked helpful 0 times.

@jpaulson What do you mean by the numbers are big enough? If a serial program is parallelized to use 4 cores, but your program ends up spending half its time synchronizing, then the cost might be significant and it might be worth doing something about it like what is mentioned in the next slide.
This comment was marked helpful 0 times.

It was not specifically brought up, but one other problem I imagined that might occur with a work queue is that the hardest piece of work is removed from the queue last - then every other worker sits idle while the one worker tackles the large problem.
It would've been more desirable to start the hard work up front, and then knock out the "easy" work in the mean time
This comment was marked helpful 0 times.

serialization in this program is the ratio of the sum of the black regions and the sum of the blue region.
This comment was marked helpful 0 times.

@LeeK What jpaulson is pointing out is that the larger the potential primes are, the greater the proportion of time the threads spend in is_prime (since the runtime of is_prime is logarithmic at best)
This comment was marked helpful 0 times.


In this example, we speculated that the cost of the critical region (the locked portion of the previous code) was taking up a large portion of the program's run time. To resolve this issue, we modified the counter to increment by a larger amount, so a single thread is now responsible for checking multiple numbers, but there are fewer sequential pieces of code.
This comment was marked helpful 0 times.

I'd like to clarify the discussion we had in lecture:
I think it's better to say that by increasing granularity, it is possible to reduce time spent in the critical section. Increasing granularity has two benefits:
It reduces overhead. The
lockandunlockoperations above constitute overhead that does not exist in the sequential version of the program. By increasing the granularity of work assignment, the program takes the lock fewer times, and so this overhead is reduced.It reduces the likelihood of contention for the lock, or equivalently... it reduces the likelihood thread execution is serialized within the critical section. I was a bit loose in lecture when I called the critical section "sequential". Really, the critical section only triggers sequential execution of threads that are trying to enter it at the same time. Threads that are performing other work, such as executing
test_primality, can certainly be running in parallel with a thread in the critical section.
This comment was marked helpful 0 times.

I think it would also be safe to say that for most random distributions for the cost of jobs, increasing granularity will also tend to decrease the variance of the length of time each thread spends computing between critical sections, at the cost of increasing the expected value of that interval. Whether this is good or bad may vary with load, but is secondary to the reduction in synchronization overhead.
This comment was marked helpful 0 times.

By increasing granularity, we allocate a larger amount of work to a thread per time. If the total number N is large enough, it always works well. For small N, it may cause unbalanced workload distribution.
This comment was marked helpful 0 times.

@xiaowend How does it always work well? You'll still have an unbalanced workload if one of a million processors takes 1000 times longer than the rest (this could actually happen). Then you'd still have to wait on the processor that unfortunately ended up with the most work.
This comment was marked helpful 1 times.

@kfc9001 You are right. I should have assumed the case is 1:N is large enough, 2:each workload are almost equal.
In fact, I intended to say larger granularity may lead to unbalance workload.
This comment was marked helpful 0 times.


Would an apt example of machine restriction be the following? CUDA with compute capability 2.0 allows only 1024 threads per block. Hence the number of subproblems within a block gets restricted to either this number. If not, we would have to handle the subproblems in chunks of 1024 which may cause an overhead problem, like in assignment 2.
This comment was marked helpful 0 times.

Just as what the slide says, there should be many more tasks than processors (in this case more than 1024 for each block) so that dynamic assignment has a large enough work pool to choose from. But the number of tasks should not be infinitely large because once the workload of each task gets small, overhead of managing the tasks will dominate the useful work, and doing MUCH MORE work to guarantee a better workload balance is surely a bad thing to do.
This comment was marked helpful 0 times.
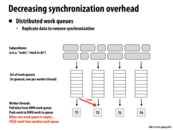

To decrease the overhead in synchronization, we can create work queues for each processor. The processors would push or pull from their own work queues, and if there are no more tasks in their queues then they will steal tasks from another processor's work queue. However, when stealing a task they need to ensure that they do not disrupt that processor. By implementing distributed work queues among processors we can have high locality (since the tasks are created and stored in the processor itself) and we will reduce the communication among processors. This is a good implentation of an efficient virtually-shared work queue.
This comment was marked helpful 1 times.

One way a processor can steal a task without disrupting the other processor is taking tasks from the opposite end of the queue. So if T2 is taking tasks from the bottom of the queue, T1 can steal tasks from the top of the queue.
This comment was marked helpful 0 times.

@hh I think this might also lead to synchronization problems. Consider the situation when 2 processors want to steal tasks from the same processor at the same time - a lock is definitely needed in this situation to ensure mutual exclusion. Also, we may want to insert a new task into one of the task queues, which also need to be synchronized.
This comment was marked helpful 0 times.

You still need to synchronize access to the end of the queue, but contention is significantly reduced. In addition, it's possible to implement block-free queues using hardware support via bus locking or load-link/store-conditional operations.
This comment was marked helpful 1 times.
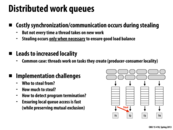

I think a way to reduce the overhead of synchronization could be to use the idea of "try_lock". We can keep a global number of how many tasks, in average, are left in each of the processor's work queue. Then, when a processor finds out that the tasks left in its work queue are less than the average, it will try to steal some tasks from other processors. However, as the idea of "try_lock" suggests, this processor will just attempt to acquire the lock of other processor's work queue once. If it succeeds, it will steal some tasks. If the lock is currently acquired by other processors, it will give up immediately and back to do its own task - and try to steal tasks later. For those processors that have more tasks to do than average, they will not even try to steal but focus on finishing their own tasks. This design can answer the question of "how much tasks to steal" - just steal up to average. Also, we can do useful work when we need to wait for the lock, which, in some sense, reduce the overhead of synchronization (think increasing granularity). However, this design also have problems. We need extra work to update the average tasks. And we need even more work to determine who to steal from. And most importantly, processor may be starved because there is no guarantee that it will eventually get the lock.
This comment was marked helpful 1 times.

I think the distributed work queues approach shares the same problem with the smart task scheduling approach mentioned in the next slide. In order to determine how much to steal in the distributed work queues approach, the processor need some notion of how much workload each task provides, and steal only enough work to keep itself busy. If we record a global average task count as suggested by @bosher, and keep stealing to keep an average number of tasks to do, we will find ourselves over-stealing/under-stealing in terms of workload, and the result would be tossing tasks back and forth between processors, which is expensive given the synchronization overheads. Similarly, the crucial component of implementing a smart task scheduler is to know the workload of each task beforehand (or at least come up with a fairly good prediction), and schedule the heavy tasks first.
This comment was marked helpful 0 times.

@bosher The problem with only using try_lock is that you might end up with starvation: a processor that consistently has a lot less work than others can keep trying to steal work, but keep failing because try_lock doesn't ensure bounded waiting (i.e. there is no guarantee that the processor will ever succeed in getting more work). If you take this to the extreme, you could have many processors sitting around doing nothing, repeatedly trying to use try_lock, and consistently failing (perhaps due to how the lock is implemented). Then you aren't make good use of those processors at all, and it might have been worth using normal locks and incurring the cost of communication overhead, because at least you won't be letting processors sit idle (and thus decreasing total execution time).
This comment was marked helpful 0 times.


If we schedule these tasks onto free processors in left to right order (as shown on slide 34), then the longest task will be computed last, reducing the overall efficiency of the program. The other processors will be idle because all other computations have finished so they will just be waiting on this last one. A solution given on slide 35 is to schedule the longer tasks first so the other processors can 'pick up the slack' while there are still tasks to completed. (Note this requires some predictability of cost the work.)
This comment was marked helpful 0 times.


If we schedule the tasks from the previous slide in left to right order, we may get a schedule resembling the one above. P1-3 will need to wait for P4 to finish the last large task before the program can continue execution. This helps show the importance of granularity in task assignment. If we know the granularity of different tasks ahead of time, we can get a large performance increase by scheduling those tasks first.
This comment was marked helpful 0 times.

Having prior knowledge of workload allows for more efficient task scheduling; essentially, if we schedule the longest task first, we can run other tasks on other cores and avoid having to wait for this tedious task at the end.
This comment was marked helpful 0 times.


If you consider the worst case as one core computing your longest task and the rest sitting idle, scheduling the long tasks first gives a better load balancing because with every task you assign your worst case performance decreases.
The reason that you can't always do this is that you need to have some idea of which task will take the longest. If you don't know how long the tasks will take relative to each other, you can't come up with a good ordering.
This comment was marked helpful 0 times.

Question: In OS scheduling, the running time of processes can be predicted by looking at their past records. I wonder how workload of tasks can be predicted here?
This comment was marked helpful 0 times.

Compared to the time taken in the previous slide where P1-P3 finished the work first and waited for P4 to finish the last long task, this new scheduling order helps balance the workload a lot better, as P1-P3 take more work on while P4 focuses more on the long task. However, we need some knowledge of the workload (specifically, the expected runtime of the tasks) in order to perform this scheduling optimization. Therefore, predictability in time needed to finish the task is important.
This comment was marked helpful 0 times.

Implement good schedule even we can use distributed work queue so that we can reduce overhead of redistributing work
This comment was marked helpful 0 times.


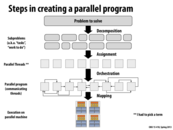









This slide gives a big-picture overview of the process for turning a problem into a parallel program.
The decomposition step involves breaking the problem into independent subproblems. More subproblems will increase your maximum potential to parallelize the computation. At this stage, the division of work is based on the constraints of the problem, not yet focusing on the implementation and hardware.
The assignment step involves mapping these subproblems to an abstraction in the program. Examples of this include pthreads, ispc tasks, and CUDA blocks/threads.
The orchestration step involves using some method of communication between tasks. We have discussed shared memory and message passing as options for doing this. As we have seen, communication can lead to tasks waiting to access shared memory or to receive a message, so poorly implemented communication can severely detract from the performance of a program.
Finally, the parallel program is mapped to the hardware it is run on. This varies based on details such as the number of cores, the width of the lane for SIMD execution, and the CUDA warp size. Depending on the method chosen, the programmer may have little control over this step.
This comment was marked helpful 0 times.