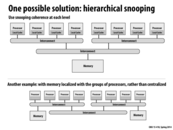

I see a potential benefit in the first one, in that each time a processor broadcasts, it doesn't have to send it to so many processors. This allows for scaling of the broadcasts. However, I imagine that if suddenly a processor on another interconnect wanted to do something with the cache line that a processor on another interconnect already modified, then there will be overhead in getting visibility of that modification to the new processor. Thus, I would believe that thrashing becomes even worse in this case. In the second example, having different memory banks could be weird if some memory needs to be shared between processors on different interconnects. In that case, I suppose they could be duplicated in memory, and this in itself has a lot of overhead.
This comment was marked helpful 0 times.


A demo was shown in class:
A bunch of people represented "processors", which requested data from memory, labelled either X or Y. Whenever someone wanted a request, they "shouted" at the interconnect. In parallel, this represented a lot of people yelling at Kayvon.
When a processor wanted to "write" to X, they had to yell at ALL the other processors and tell them to invalidate X from their cache. This was a mess, and it didn't scale well.
To resolve this problem, we added some people, who represented memory "directories". The "X directory" kept track of all the people sharing X. Thus, when someone wanted to write to X, only the "sharers" of X were notified. This scaled in a much better way than everyone shouting over the interconnect!
This comment was marked helpful 0 times.
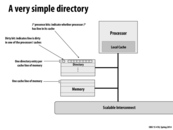

Just curious, what exactly defines a "scalable" interconnect? Does that just mean it can handle an arbitrary number of processes shouting over an interconnect, or does it have some other special scalability properties that make it efficient?
This comment was marked helpful 0 times.

It means the design can scale to handle the high amount of traffic that results from serving many cores. We'll talk about the design of interconnection networks later in the course.
This comment was marked helpful 0 times.
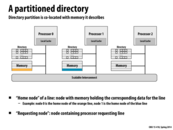

Here, a lot of memory is needed to store the directory info. If the cache line is 64 bytes and there are 64 processors. Then every 64 bytes in the memory needs at least 8 bytes in the directory. So we need to copy 1/8 of the whole memory into processor memories. How could it possibly be?
This comment was marked helpful 0 times.

@paraU:
We spent a good portion of the latter half of this lecture discussing this issue. Some possible solutions included encoding cache directories as:
1) limited pointer schemes (linked lists of processors using each line),
2) bit vectors (2D arrays of processors vs number of lines in memory, where a single bit represents "present"),
3) sparse directories (pointers for each line being accessed in cache. A pointer points to processors N's cache (where N has the line), and inside the cache of processor N, there is a pointer to processor M's cache (where M has the line), etc...),
and more!
This comment was marked helpful 0 times.


I'm not quite sure I understand how directories are kept coherent. Should each processor's directory be kept the same (i.e. if we update one directory, do we have to update the other ones?) Or is it that each directory entry is kept up to date? (Or is it something else entirely?)
This comment was marked helpful 0 times.

The memory attached to each processor is just a segment of the entire address space and each directory is only responsible for that segment. If Processor 0 wants to get a variable out of Memory 1 it has to go through Directory 1. Since every address is only managed by a single directory there's nothing to keep coherent.
This comment was marked helpful 3 times.

What if Processor 0 needs to make lots of reads to, say, a 20MB array stored in Memory 1. This array is too big to fit in entirely in P0's cache, so P0 would have to go to M1 for it almost every time. Would you just want to avoid directory-based coherence given this application? Or maybe the best thing to do in this situation would be to delegate all of P0's tasks on this array to P1?
This comment was marked helpful 0 times.

Going back to a lecture from long ago, the best solution would probably be to force a mapping of the task that reads the data to the processor that holds the data in its memory. I'm not too sure how this would be done, however.
This comment was marked helpful 0 times.

Up to my understanding, coherency is maintained by continuing to use the MSI states for each processor's cache, but instead of shouting to everyone, they use the directory to only send updates to cores processors that need it. So, coherency is the same as in MSI but with minimal shouting.
This comment was marked helpful 0 times.


I'm curious about the amount of traffic going through the interconnect here. As these messages are targeted to a single processor or two processors, wouldn't this impose a large load on the interconnect?
This comment was marked helpful 0 times.

Yes it certainly will! Especially for reasons we discuss in lecture 16, each message is in itself serialized. Think about how for each red line above, the requester needs to first ask for permission to 'have' the bus, then the arbitrator assigns permission for the requester, then the address is sent on the wire, and so on... this is most certainly a huge load on the interconnect!
This comment was marked helpful 0 times.


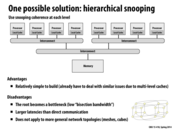
Comparing snooping to directories, snooping protocols tend to be faster since if enough bandwidth is available, all transactions are a message seen by all processors. However, snooping is not scalable. Each request has to be broadcast to all nodes in a system, meaning that as the system gets larger, the size of both the bus and the bandwidth it provides needs to grow for us to maintain speed.
Directories tend to have higher latencies (using more messages each write or read) but use much less bandwidth as messages are not broadcast to all processors but rather from one point to one point. Thus, many larger systems use directory based cache coherence.
This comment was marked helpful 0 times.

So does it mean, according to the last sentence on this slide, if there are a lot of sharers trying to read and write data simultaneously, all caches are communicated at the same time, snooping based cache coherence could beat directory based coherence because it has fewer overhead of intercommunication and lower latency?
This comment was marked helpful 0 times.


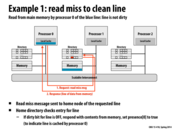
As Kayvon mentioned in lecture, in practice, for most datasets, only a small number of processors are sharing a particular cache line. Because of this, there is a significant advantage to using point-to-point communication versus broadcast communication for cache updates. For example, we may only need to communicate with 2 other sharers instead of all 63 other processors for broadcast.
This comment was marked helpful 0 times.

As the next slide mentions, there is a small percentage of lines that are shared among many processors, such as the root node in Barnes Hut. This can be seen at the very right-most bucket of each histogram. However, these lines do not tend to present an issue to directory-based cache coherence performance, because they are not frequently written to, and instead mostly read.
This comment was marked helpful 0 times.


In my opinion, the high-contention lock case is kind of a moot point because once there are many contenders for a lock, those contenders are stalled waiting for the lock, so if performance of the cache system is low (causing cores to wait), it isn't all that terrible - the high-contention lock should be eliminated by the programmer anyway.
This comment was marked helpful 0 times.


For bit vector directory representation we need a P bit vector to represent whether each processor has a line of cache cache. For M line cache we need total P * M amount of storage. We could scale with above representation but as stated in the slide, we would use a lot of memory space. Thus, we need to consider other approaches such as limited pointer schemes and sparse directories.
This comment was marked helpful 0 times.


As from last lecture, we see that increasing the cache line size (which would reduce the M term and reduce the storage overhead) may result in an increase in cache misses due to false sharing (see lecture 11, slide 9), increasing overall interconnect traffic (see lecture 11, slide 11).
This comment was marked helpful 2 times.

@bstan, great post. To clarify it, I'd like to add that you just gave two different reasons why it might not be good to increase cache line size: (1) potentially more misses due to false sharing and (2) potentially higher bandwidth requirements (to memory and thus on the interconnect). I want to make sure one does not interpret your post as saying that misses might go up, and thus you'll see increased traffic if that is the case. A program can experience higher traffic (e.g., have higher memory BW requirements) with increasing line size even if the total number of misses goes down. This is because with the large lines it is less likely that all the data in a line is actually used by the program, and thus extra data is transferred. In other words, with increasing line size a program must have increasingly high spatial locality in order to avoid transferring unnecessary data.
This comment was marked helpful 2 times.


How easy is it for a system to switch between point-to-point and broadcast communication or revert to a bit vector representation? Wouldn't switching between the different methods and having to initialize them each time you switch have a huge time penalty, especially if the switch occurs often (kind of like thrashing)?
This comment was marked helpful 0 times.

@asinha There won't be a time penalty because you won't need to reinitialize anything. You could potentially have bit that represents the protocol you will be using. In this case when you go to use the directory scheme you check this bit and determine if you should use a broadcast or attempt to only communicate with the processors needed.
This comment was marked helpful 0 times.

I think there might be some overhead still even if you can simply switch to the broadcasting method. For example, the directory control system still needs to be updated even if the system is using broadcasting at the current step in the event that the shared count drops below the the broadcasting switch threshold.
This comment was marked helpful 0 times.

How is it determined which of these fallback methods is implemented? Is one better than the others depending on the machine? It seems like it would depend on the applications, for example on how many nodes the application uses and how far over the max number of sharers the application will go.
However, it seems like a waste if we go one node over the max number of sharers and it instantly switches to broadcasting. Like I said above, it probably depends on the application, but to me the best fallback method seems like the third one. It seems like it would be relatively easy to implement a system where if we have max+1 sharers, each bit would represent 2 nodes, and then as soon as we have 2*max+1 sharers, each bit would represent 3 nodes, etc.
This comment was marked helpful 0 times.


This is a very silly idea, but if we want a data structure to efficiently store the pointers (sharing processors) each of which can be represented by log P bits, we can build a binary decision tree on the set of pointers. Every bit for the pointer leads you down a branch and at the leaf you mark the path you go that get you there as either exist or not exist. To implement this in a low level manner, one can store the tree in the in-order traversal. The traversal can be characterized as a string of characters where a character represents one of BRANCH0, BRANCH1, EXIST or NONEXIST. You can implement a character with two machine bits. Pros: Binary decision tree allows us to not store the overlapping bits in two pointers. When we have a huge number of processors, so big that even log P starts to hurt, this scheme may potentially store more pointers compared to limited pointer schemes, using the same amount of space. Just as limited poitner schemes, binary decision trees takes up less space compared to a full bit vector when entries are sparse, but in the worst case, to store all the pointers, you'll have a complete binary tree of depth log P, which takes O(P) bits (not P bits alas) which is better than O(P log P) for limited pointer schemes Cons: Great pain to do a look up, may require additional space to do so. For small P and even sparser entries in the directory, this takes more space than limited pointer scheme. Silliness of this idea is also a con.
This comment was marked helpful 0 times.

That's a really interesting idea, but wouldn't storing the binary decision tree take a constant $2P - 1$ bits of space (ie. $\sum_{i = 0}^{\log_2 p} 2^i = 2P - 1$)? To store a binary tree in a flat array, the children of the element at index $i$ would be located at $2i + 1$ and $2i + 2$, so the final level of the tree would be at bits $P - 1$ to $2P - 2$.
Did I misunderstand something in your description?
This comment was marked helpful 0 times.

That's one way to store the binary decision tree, which is treating it as a complete binary tree (just like what we did in 122), and yes it will take O(P) space. So I thought we need to store it as an in-order traversal (or pre or post order traversal, if you like) which takes up O(nodes-in-the-tree) space. I have the details of the implementation written in my previous thread.
This comment was marked helpful 0 times.
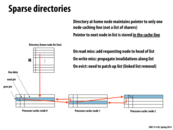

There was a question in lecture about this and I didn't quite catch it. It doesn't seem like this is shrinking M rather than P. Is that right or am I misunderstanding the sparse directory implementation? Thanks!!
This comment was marked helpful 1 times.

@Yuyang: Yes, that was the question in lecture. My answer is that in spirit, in a sparse directory scheme, a list of sharers is only stored for lines that happen to be cached. In this sense, the directory is sparse in lines (rows) and thus we've shrunk the number of rows M.
A say in spirit because as I describe it here, there still is a head pointer per line in memory. So there's still of O(M) storage, but the constant is much lower since the per-line storage is just a single processor identifier (the head of the list).
Make sense?
This comment was marked helpful 0 times.

So this is reducing the original cost of M*P to M*c1+TotalSizeOfCache*c2, where c1 and c2 are constants... Would that be accurate?
This comment was marked helpful 0 times.

@eatnow, I think it should be $$ \sum_{n=1}^i {c * p_i} $$ where $i$ is the number of lines in the cache, and $p_i$ is the number of processors that has i'th line, $c$ is the constant cost from pointer and anything else.
This comment was marked helpful 0 times.

@eatnow. I agree with your expression if TotalSizeOfCache refers to the total aggregate size of all the caches. @black. Your expression, if I understand correctly, is the same as the second term of @eatnow's if I interpret $i$ as the number of unique lines across all caches and your c is @eatnow's c2.
This comment was marked helpful 0 times.

Wait, how have we shrunk M if the formula still involves M? Am I missing sth completely?
This comment was marked helpful 0 times.

@uhkiv. See answer to Yuyang above.
This comment was marked helpful 0 times.

Okay. Let me see if I get this. M * c_1 part is to account for directory storage where c_1 is size of a pointer. Presumably, c_1 << P (is that correct?).
Also, for each cache line, you need two pointers.
However, we still need a directory entry (that stores one pointer) for each memory line, right?
This comment was marked helpful 0 times.

Yeah I see. Yeah we still have M lines but the constant for each line is smaller :D
This comment was marked helpful 0 times.


Question: is it possible to implement a tree instead, or it is too complex?
This comment was marked helpful 0 times.

I think it is possible.
This comment was marked helpful 0 times.

How much memory does each cache need to store to maintain this linked list, the total number of lines that are out there in at least one cache * log(# processors)? Or in other words, does a cache need a linked list entry for every active line in the cache?
This comment was marked helpful 0 times.

@jinghuan: Each cache line's metadata would be extended to include next/prev pointers. Each of those pointers would be log_2(P) bits.
Just to clarify, note that this information is stored in a similar manner as line metadata (coherence state, dirty bit, tag bits, eviction policy stats, etc.). I wouldn't think of this pointer data as data "in the cache", I'd think of it as an extension of all the other metadata that accompanying a line.
@k_d___g. I'm curious, why do you suggest a tree? We have to walk the list to determine all the sharers. Even if it was organized in a tree, we'd still have to touch all the nodes, so a tear-down remains O(num_sharers). There's no situation where the system searches the list for a particular sharer. If a processor drops a line, no searching of the list is necessary. The processor's cache need only follow the next/prev pointer to the next and previous caches and back up their pointers respectively.
This comment was marked helpful 0 times.
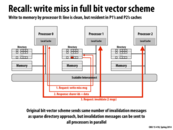

The key idea here is to illustrate the disadvantage of sparse directories when compared to bit vector directories. Although sparse directories do save space, a write miss in a bit vector directory allows for invalidation messages to be sent in parallel, resulting in a faster acknowledgment and overall write speed than the sparse directory format where traversing the linked list of sharers to invalidate each one is necessary. I would imagine this is more of a problem in computers with an extremely large number of processors, where the linked list of sharers for a single cache line could be very long. If, however, we are considering a quad-core machine, then the write latency probably would not be as significant.
This comment was marked helpful 0 times.
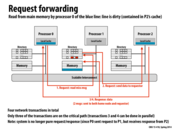

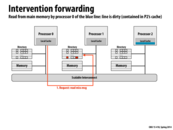
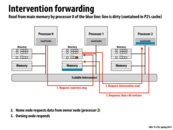
In class we walked through a couple of scenarios like this, incrementally decreasing either the length of the critical path or the total number of messages. This particular slide has a critical path of length 3 with 4 messages. P0 asks P1 for some data, but the response to P0's request actually comes from P2. This eliminates the latency of the response going through P1 to get from P2 to P0.
This comment was marked helpful 0 times.

So something I was thinking about was whether or not this method was faster or slower than simply updating each processor. Surely, there is a great benefit from not having to crowd the the interconnect, but by updating each processor, the critical path (in span) would be 2 correct? One processor sends a message to each other and waits for a response from each of them. Ideally, this could be faster, but I guess the problem is scalability as we are getting better at packing more cores on a chip right?
This comment was marked helpful 0 times.

The entire point of the directory scheme is to avoid broadcasts if possible, as these are slow and create contention (for the bus). The directory allows us to directly address only the processors that have a cache line instead of all the processors. Your scheme would make the directories pointless by requesting a line from all processors.
This comment was marked helpful 0 times.

A potential problem for this implementation is the irregular pairing of send and receive. For processor 0 in the slide, it sends a request to the directory of processor 1, yet the response is from processor 2. It's not like the regular scene where send and receive only involve two participants and may need more complex strategy to handle the response.
This comment was marked helpful 0 times.

@squidrice: Instead of looking at which processor ID a message was sent to/received from, the requests and responses can be tagged with a request ID. That could be a counter, which raises the problem of how such a shared counter would be maintained, or a random 32-bit number (which raises the problem of collisions, I suppose).
This comment was marked helpful 0 times.

benchoi - maybe if you have P processors, each processor could keep track of how many messages it's sent out and label each message's ID as P*x + n, where x is the number of messages that processor has sent out and n is the unique label of the processor.
So for example, if we have 7 processors, processor 0 would label its first message 0, its second message 7, etc, while processor 1 would label its first message 1, second message 8, etc.
This way we just need to assign each processor a number at the start and have each processor locally keep track of 2 numbers, and we'd guarantee that every message had a unique ID (plus you could figure out which processor the message came from just by looking at the ID)
This comment was marked helpful 0 times.


It doesn't seem possible to achieve the "best" scheme for all cases, and so we have to consider our goals. The directory is scalable and reduces broadcasts, but in a small enough system, broadcast is just fine. And avoids the challenges of directory-based coherence, which also has the same issues as broadcast in the uncommon case.
This comment was marked helpful 0 times.
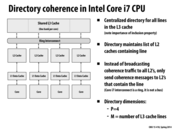

If L3 does not have the data requested, could any L2 have that data? How does L3 include all data from L2? Who is maintaining the 4 bits and copying data from L2?
This comment was marked helpful 0 times.

Because of inclusion, if L3 does not have data, then any L2 could not have the data.
Maintaining inclusion is harder than intuition, which briefly talked in previous lecture.
Cache directory maintains the information, and it depends on where you put the directory.
This comment was marked helpful 0 times.

I'm a little curious about how the different levels of cache maintain data. I understand that L3 needs to have the same data as L2 (by inclusion), because if something is evicted from L2, it then needs to be there in L3 so that a memory fetch doesn't occur. However, this seems like a huge waste of space, because of all this duplication. It almost feels like once you've included everything in L2 in L3, there isn't much space left in L3 for other data. Is this generally true?
This comment was marked helpful 0 times.

The geometries of an Intel Core i7 cache hierarchy are given here. The per-core L2 is 256KB, and the per-core slice of the L3 is 2MB. So the aggregate size of the L2's across all cores is 1/8th the size of the L3.
Or you can think about it as the L3 being 32 times larger than any one L2.
This comment was marked helpful 0 times.

@idl, there are different cache designs, and there have trade offs. For example, there are inclusive and exclusive caches. Exclusive caches would guarantee that data would be only in one of the cache hierarchies, which means if the data is in L1, it can not be in L2. In this way, space is saved, but cache has to search all the way to L1 for coherence.
This comment was marked helpful 1 times.

After reading @yanzhan2's comment about exclusive caches, I read a bit more about them as I hadn't heard of such a design. I found that both types are used in processors (see AMD Athlon for exclusive cache), as well as intermediate policies that aren't strictly inclusive or exclusive (see pentium 2,3,4). It all seems pretty arbitrary, but it seems that the inclusive policy is winning out in the latest high-end processors, as memory is less of a concern.
This comment was marked helpful 0 times.



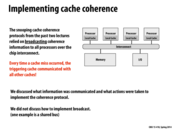














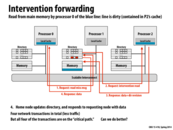
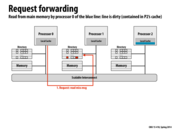
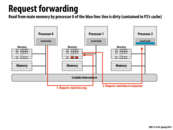
For answering those questions, I think: 1. The scalability of snooping-based cache coherence implementation is limited by broadcast traffic for intercommunication, even though it has lower latency. 2. Directory-based scheme avoid this problem by introducing directories that store the information of cache line, so that cache coherence is maintained by point-to-point messages instead of broadcast. 3. There are two alternative implementations other than bit vector which has high storage overhead: limited pointer schemes and sparse directories, at the cost of the increase of complexity, increase of latency.
Please correct me if I missed anything...
This comment was marked helpful 0 times.