

@Question I was just curious. Is there a more formal-sounding definition of "throughput"? Intuitively I can see what it means but it would be helpful to define it carefully (it can sound like 1/latency, for example)
This comment was marked helpful 0 times.

Throughput is simply a general term describing the rate of completion of operations.
For example bandwidth (bits/sec) is a measure of throughput. Jobs per second is a measure of throughput.
This comment was marked helpful 0 times.
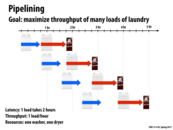

Notice that we are constrained by the scarcest resource (with only 1 dryer, you can't beat one load per hour). Even if we had an infinitely fast washer, it wouldn't help at all.
A pipeline is only as fast as its slowest link!
This comment was marked helpful 0 times.

Pipelining is the idea of starting the next operation before the previous one completes. This can be used when there is parallelism between the operations. In this example, we have more than one loads of laundry, so clothes can be placed into the washing machine while the previous load is still drying. The latency is limited by the hour it takes to use the dryer.
This comment was marked helpful 0 times.

Notice that in fact, we are constrained by the slowest resource. After the clothes finished washing, they need to wait for drying. The time duration between clothes finishing washing and starting drying becomes longer and longer.
This comment was marked helpful 0 times.

@xiaoend: You said: "The time duration between clothes finishing washing and starting drying becomes longer and longer." This is certainly true in the diagram, but consider where those wet clothes go? If your college dorm is anything like mine was, basically they sit on top of the washers until dryers become available. In essence, you stick the wet clothes in a buffer. (And hope happens to knock the buffer on the floor.)
If the washer keep washing at its peak rate, that pile of clothes waiting to be dried is going to grow and grow. This is because since wet clothes get added faster than clothes get put in the next available drier. At some point you have to stop doing wash, because there's no place to stick new wet clothes, the buffer is full! (So you probably leave them in the washer.) See slide 11 for an example that's a little more computing oriented.
This comment was marked helpful 0 times.


The key idea from this slide is that even though each instruction always takes 4 cycles (in this example), we can still perform n instructions in roughly n cycles. Because we split up the instruction into multiple steps, just as we split laundry into the washing and drying steps, we can do different steps for different instructions at the same time. We cannot make the latency of the instruction lower than 4, so one instruction will always complete 4 clocks later. However, since we can perform one step of at most 4 instructions at the same time, if we supply new instructions once every cycle, we will complete an instruction once every cycle. This gives us a throughput of 1 instruction per cycle.
Compare this to latency hiding from previous lectures, where we could context switch among threads so that we could work on one thread while waiting for a memory retrieve for another thread.
This comment was marked helpful 1 times.

Pipelining has been a great way for speeding up the execution speed of a program but it's up to the programmer to fully utilize it. Using a lot of conditionals in one's code can hurt the pipeline because it can force the processor to branch to some location in memory and flush out what's currently in the pipeline (unless the branch predictor correctly guessed which branch the program will take) which then has start fresh at the next instruction. Assuming that there's 4 cycles per instruction, each branch effectively adds 3 extra cycles for each missed branch.
This comment was marked helpful 0 times.

Instruction pipeline is a great technology, but it is hard to be utilized fully when design CPU. The ideal situation for this graph seems to be 4x speedup, but several reasons make it difficult to realize. First, if the pipeline is stopped, it needs some extra cycles to recover, as tliao said. Second, because of all stages should be finished in a cycle, the length of a cycle equals to the time used by the slowest stage, which drags the progress of other stages down. For efficiency, long stage may need to be split. Last, dependency may exist between two instructions, which leads to complicate synchronization methods.
This comment was marked helpful 0 times.

Question: Let's say the "execute" phase of the above pipeline took significantly longer than the other pipeline stages. What might you consider to speed up the pipeline's execution?
This comment was marked helpful 0 times.

@kayvon If any one portion of the pipeline takes a disproportionately large amount of time, we could add more of the relevant units to break up this work. For this example, we could add a second execution unit and have the decoder alternate feeding one EU and then the other.
This comment was marked helpful 0 times.

Shouldn't a good instruction pipeline be designed so that it can never be the case that one stage is significantly longer than the other pipeline stages? Suppose a stage A is longer than any other stages in a pipeline, then once A's buffer is full, execution of other stages will pause for A's buffer to be available again. So why not put some of the execution units of those fast stages into the slow stage to balance the execution time instead of wasting them knowing that they will pause every once in a while?
This comment was marked helpful 0 times.

^ Balance the load between different stages of a pipeline is indeed a good design heuristic. However, there are certain things you just can not avoid. Usually the most time consuming stage in a pipeline involves memory access, which can be >100X compared to operations such as decoding etc.
This comment was marked helpful 0 times.


An advantage of buffering is to decouple your producer (yellow boxes) and consumers (blue boxes). In this example, the producer will send a burst of messages into a buffer (until that buffer fills), and then wait for the consumer to finish processing before doing so again. This is helpful because the producer is no longer as dependent on the consumer, and can go about it's business until it is needed again.
This comment was marked helpful 0 times.

In "steady state", buffering actually doesn't help at all (the buffer just gets full). But if the slow pipeline is just a temporary condition (the producer is sending an unusually large burst of messages or the consumer is under high load), buffering does help!
Buffering reduces the costs of high variability pipelines (most real pipelines are high variability)
This comment was marked helpful 0 times.

The steady state refers to when the user is sending infinite number of messages. the advantage of buffering is to decouple producer and consumer. it may not helps decrease the absolute cost of communication but it definitely increases overlapping and does useful work in between.
This comment was marked helpful 0 times.

I think buffer can decrease the absolute cost of communication even in steady state.
If there is no buffer, after the consumer finishes one piece of work, the consumer need to wait for the producer to find out it can use consumer again. The consumer may find there is no work for it to do for a short time every time it finishes a piece of work. This may actually increase the time for consumer to finish a piece of work and reduce bandwidth.
Is this correct? I am not sure.
This comment was marked helpful 0 times.

@TeBoring well let's just say that after the buffer can hold at least one piece of work, further increasing its size won't decrease the absolute cost of communication in steady state. But again we are not math majors and shouldn't be concerned with the theoretical values. As @jpaulson suggests, when the slow pipeline is just a temporary condition, buffering (and the size of buffers) really matters.
This comment was marked helpful 0 times.


Inherit communication is necessary communication that must happen for the program to work. In this example, P2 must receive the rows highlighted in red from P1 and P3 in order to compute the correct values for its top and bottom rows, respectively. Otherwise, the algorithm will not be correct.
This comment was marked helpful 0 times.


It is important to remember that decreasing the communication to computation ratio might not always lead to better performance. (A single processor has ratio = 0, but might not be fastest) In this example, there is a trade-off between parallelism due to an increasing number of processors vs higher communication to computation ratio.
This comment was marked helpful 0 times.


Block assignment reduces the perimeter of the assignment for each processor. However each processor still computes N^2/P elements like before. Reducing the perimeter reduces the communication cost since there are less elements that need to be sent between processors.
This comment was marked helpful 0 times.


The reason arithmetic intensity is more intuitive is because it follows the "more is better" convention. A higher arithmetic intensity means lower communication overhead, which is a good thing. It's Kayvon's personal preference, but it makes sense.
This comment was marked helpful 0 times.


Here, we are introduced to the notion of artifactual communication, so named because it's "an artifact of how the system is implemented". While inherent communication costs are directly associated with the operations of the algorithm, artifactual communication describes all other costs incurred in the execution. For instance, when we attempt to load an int from memory, the inherent communication cost is that of moving a single int, but since the system will load a full cache line during this operation, the artifactual communication cost is that of loading the cache line.
This comment was marked helpful 1 times.


Explanations of the misses in a little more detail:
Cold Miss: Occurs when the cache is empty or the data you are trying to access has not yet been loaded into the cache. As it says in the slides, this is an unavoidable miss and there is nothing a programmer or architect can do about it.
Capacity Miss: The data has been evicted from the cache and is no longer accessible. Aside from changing the ordering of the cache eviction (assume the ordering is ideal), this can be fixed by both the programmer and architect by: (Programmer) Change the program to access the data earlier, so right after storing it in the cache, perform the computation that requires that data before storing even more data in the cache and causing possible eviction. (Architect) Build a bigger cache.
Conflict Miss: The cache has a poor eviction order so the data you are trying to access is constantly being evicted due to conflicts from other pieces of data. Recall that data is placed in certain places in a cache based on its set bits. This can be reduced by changing the cache's placement and eviction policies.
Communication Miss: In a parallel system, a processor computes and stores data that a different one needs, so every process that requires the data must compute it on its own.
This comment was marked helpful 0 times.


The capacity should be just large enough to fully encompass some integer number of working sets since you get the greatest decrease in misses per unit capacity immediately preceding those points. (A capacity level right after the sections of steep dropoff on the graph.) Basically, fitting an entire "section" of data in the cache is important so you don't have to remove any data that you will reuse immediately and often.
This comment was marked helpful 0 times.

Elaborating on @Xelblade's explanation, from a cache designer's perspective it is important to maximize perf/cost efficiency (transistors do not grow on trees). Therefore when choosing adequate cache sizes, the designer will more often than not choose the points right after the drop-off happens, since these points produce the most noticeable change in data traffic.
This comment was marked helpful 0 times.


One thing which was unclear to me from just this slide alone during lecture was the access pattern of the program under discussion. Knowing that the program accesses the rows both above and below the row it's currently working on is important for understanding this slide's point about blocking for temporal locality (since cutting it into blocks of four, as on the right side, lets you re-use the current row and row below it during the next iteration, which gets you two cache hits instead of two misses later if you use the left-hand row-major strategy).
This comment was marked helpful 1 times.

Using the technique on the right will decrease capacity misses because it can load an entire area in the z formation and complete the calculation for that area, so only the elements on the border will need to be used again. This does assume that the grid is large enough that if you finish one row and go the the next, that previous row will probably not be in cache any more (because of a capacity miss)
This comment was marked helpful 0 times.


Co-locating cooperating threads can actually reduce cold misses because multiple threads will share the same piece of data and only have one miss for it, instead of each of them missing.
This comment was marked helpful 0 times.


This slide shows that the grid layout shown on slide 15 would experience artifactual communication costs related to the size of a cache line. This is because some of the elements that need to be communicated for correctness of the algorithm (inherent communication) are adjacent in memory to elements that are not needed for the computation. Since the system does not have the granularity to transfer just a single byte (or element), all of the elements in the blue box will be transferred together.
The 1d blocked assignment on slide 14 has more inherent communication, but when implemented would have less artifactual communication than the grid layout.
This comment was marked helpful 0 times.


In this scenario, P1 and P2 access elements that are on the same cache line. Even though they're modifying different elements, both processors cannot write at the same time, since one processor may overwrite the work of the other processor.
This comment was marked helpful 0 times.

In this example, even though computation only requires one data element, in fact artifactual communication may still occur when the data p1 and p2 processes happen to be in the same cache line. Cpu would insure cache coherence in the hardware level, while Gpu may not perform as expected as it doesn't have cache coherence.
This comment was marked helpful 1 times.


What is shown here is that greater spatial locality can be achieved and interprocessor commuication can be reduced by switching to a non-row-major-order mapping of grid elements in memory. This requires the programmer to be more clever with their indexing math.
This comment was marked helpful 0 times.

It is the job of the user to represent the cache line in the second diagram. The cache line will stay the same, but instead of having a line of [(0,0),(0,1),(0,2),(0,3)], the user must instead put [(0,0),(0,1),(1,0),(1,1)] into the cache line. Therefore, the user must store their values in an array in a tricky way to take advantage of spacial locality on the cache line.
This comment was marked helpful 0 times.
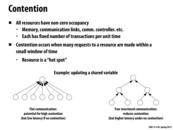

"Resource" is not just confined to variables, threads can also be resources with high contention. For example in the master-slave working model, if only one thread is designated as the master thread, all worker threads will request for work from that master thread. Then this master thread becomes a hot spot with high contention. If we modify the model so that there is a hierarchy of master threads (e.g. L1 master, L2 master...) and workers only request work from their local masters, while lower level masters request work from higher level masters, contention will be low on any one of the master threads. However, it might take a very long time for a worker threads at the bottom of the hierarchy to get new work because requests will have to travel along the path of the hierarchy tree.
This comment was marked helpful 0 times.


If different threads access same data from some place of shared memory, shared memory can broadcast it to all threads.
If different threads get data from different parts of shared memory, they can do it in parallel.
If different threads access different data from the same place at the same time, there will be conflict, called banking conflict (because the unit of shared memory is called banking)
This comment was marked helpful 0 times.

Question: Is there a typo in the code of x3?
EDIT: This paragraph is deprecated due to slide change. The code of float x3 = A[index / 2] would generate the accessing adress of 0, 0, 1, 1, ..., 15, 15. Then each bank would serve the same value twice, which could be done in one cycle.
I think float x3 = A[index * 2] would generate the accessing address of 0, 2, 4, ..., 32, 34, ..., 60, 62. Then 16 out of the 32 banks would serve two different value, which needs two cycles.
This comment was marked helpful 0 times.

@lazyplus. You're thinking is good. However, my understanding is that on the earliest CUDA-capable GPUs, two CUDA threads accessing the same value from one bank would still take two cycles. The bank is designed with the the ability to give one value to one warp thread, or one value to all warp threads. It can't give the same value to two threads in a cycle.
Since this is really confusing, what I did was change the slide to be a lot more clear. I eliminated the confusing example and went with an example, much like yours above, except I decided to multiply index by 16 to generate a very bad case that would take 16 cycles for the hardware to service.
EDIT: @apodolsk below indicates by two-cycle explanation is not correct on most modern GPUs (instead, his explanation indicates the cost of an access is proportional to the maximum number of unique values that must be retrieved from any one bank). I'll have to look into whether I was just wrong, or if the status quo is an improvement on the earliest designs.
This comment was marked helpful 0 times.

NVIDIA has some more nice diagrams:
http://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#shared-memory-3-0
Compiling rules that are scattered around the doc somewhat haphazardly, I get this set of quotes for compute capabilities 2.0 and 3.0:
(A) "Shared memory has 32 banks."
(B) "Successive 32-bit words map to successive banks." This plus (A) implies bank = addr % 32, as in the slide above.
(C) "[Different] banks ... can be accessed simultaneously." This explains case 2 in the slide above.
(D) As a bonus, "a shared memory request does not generate a bank conflict between two threads that access ... the same 32-bit word". That is, any number of threads can read a single 32-bit word simultaneously, even though they're all accessing the same bank.
Note that this is different from example 4 on the slide and in @kayvonf's post above, since that example involves reading things from the same bank and also from different 32-bit words.
(I couldn't find where it says that all threads have to write to the same 32-bit word in order for this rule to apply, for GPU's 2.0 and up. It looks like the lower-middle diagram in that link shows an instance of partial-broadcast for 3.0, and they say it's "conflict-free".)
(E) As a superbonus on 3.0 GPUs, multiple threads can simultaneously read from "32-bit words whose indices i and j are in the same 64-word aligned segment and such that j=i+32".
That is, if (arr % 64 == 0), then ((int32_t *)arr)[0] and ((int32_t *)arr)[32] can also be read at the same time.
The mental picture that I get from this is that a single bank would look like (int32_t []){arr[0], arr[32], arr[64] ....}. So one worst-case access pattern would be arr[0], arr[64], arr[128]... (It's not arr[0], arr[32], arr[64] because of rule E).
This comment was marked helpful 1 times.


A generalization of this problem is how to recursively split up 2d (or higher) space to determine regions of density before further data processing. One commonly used data structure to solve this problem is the quadtree, which is a hierarchical way of storing this information.
Quadtree construction involves many of the optimizations we see in the following slides. Additionally, quadtrees may not even fit on a single computer, and there are further interesting algorithms that dictate how to deal with that.
This comment was marked helpful 0 times.


The reason that this approach isn't faster is because each task has to do the "is particle x in cell y" computation for all 16 possible values of y in each task. Because of this, even though there are 16 parallel tasks, they each have to do 16 times more work so the result is no faster than the sequential algorithm.
This comment was marked helpful 0 times.


Here, the actual computational work for each particle (and hence each thread) is constant as one can use the grid size and cell size to easily compute which cell a particle lies in. The major time cost comes from accessing and writing into the memory. Since the memory is shared and each cell is updated by multiple threads, these updates have to be done sequentially.
This comment was marked helpful 0 times.


Since each cell can be updated independently, having a lock for each individual cell reduces contention by ~16x (there are only 16 cells in this example) compared to having only one lock for the entire cell_list. This allows different processors to update different elements of the cell_list at a given time (increasing efficiency).
This comment was marked helpful 0 times.


Solution 3 and 4 focus on reducing the contention for access to the data structure. Solution 3 on the previous slide introduced finer granularity locks, so that there was only contention when the same element of the data structure was being written to, rather than for all writes to the data structure. Solution 4 builds upon this by creating multiples copies of the grid, dividing the points between these grids, and then computing the data structure for each one. This reduces the number of accesses to the same element since fewer points are being written to each data structure. These results can then be combined for the same final result, with less contention. There is additional work and memory, but depending on the system and the particular problem, this tradeoff for faster synchronization can be well worth it.
This comment was marked helpful 0 times.

An important observation is that Solution 1 duplicates computation in order to reduce synchronization. (It completely eliminates synchronization in this case). Solutions three and four trade off memory footprint (they duplicate structures) in exchange for reducing contention. A similar idea was used to reduce synchronization in Lecture 4, when we reduced three barriers to one in the solver example.
Question: When might it be a bad idea to trade off memory footprint for synchronization/contention?
This comment was marked helpful 0 times.

If we have limited memory, then increasing memory footprint can result in reduction of parallelism. For example, when we were implementing our solution for assignment 2, initially we had allocated a bunch shared memory arrays for position, color, radius. The size of each shared memory array was proportional to the number of threads in the block. Since, we were allocating so much shared memory, we were not able to increase the number of threads per block beyond a certain point. Hence, even though we had more sub-problems and compute units available, the amount of parallelism was being limited by shared memory.
This comment was marked helpful 1 times.

@kayvonf Increasing memory requirements might be a idea on a shared memory system that potentially has a shared cache across processors (i.e. an i7). If the space requirements are much greater than in the serial implementation, there may be a lot of conflict misses in a cache that may potentially outweigh the benefits of processing in parallel.
This comment was marked helpful 1 times.


Step 3 is finding the start and end addresses of each cell segment. This step is highly parallelizable because no two threads will attempt to modify the same piece of memory.
Consider index i. The only write to cell_starts[i] happens when result[i] is the first element of that cell block. Since result is sorted, this will occur exactly once. The only write to cell_ends[i] happens when you start a new cell block. Once again, since result is sorted, this will happen exactly once. Therefore, no two threads touch the same index in the result array.
In this particular example, only index=2 will modify cell_starts[6] and only index=5 will modify cell_ends[6].
After Step 3 has run, you can use cell_starts and cell_ends to index into the array of particles which I assume has been sorted with the result array.
This comment was marked helpful 1 times.

@AnnabelleBlue -- that was an excellent explanation of the algorithm and its invariants. Very well done. (We prettied up the code references in monospace using Markdown to make it easier to read.)
This comment was marked helpful 0 times.








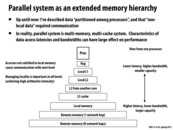






It might seem like latency and bandwidth are almost the same; you might think bandwidth is 1/latency (the # of requests you can serve is inversely proportional to the amount of time per request)
But in fact, they are totally orthogonal, because you can start the next request before the first one completes. To take the example from class, imagine students running down a hallway. The latency is the length of the hallway (how long it takes one student to complete). The bandwidth is the width of the hallway (how many students can run at once). If you imagine a very large crowd of students, you can see that (hallway width) of them are crossing the finish line each second, no matter how long the hallway is. So bandwidth is independent of latency!
This comment was marked helpful 1 times.
The definition of cost here is the effect of latency, bandwidth or other potential difficulties on our program at runtime. For example, a memory reference might have high latency but it may be improved upon by multi-threading and as a result, there would be no real cost on the program.
This comment was marked helpful 0 times.