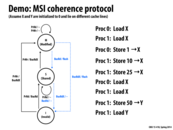

Here, X and Y refer to addresses on different cache lines (you can just think of them as different cache lines). Both Proc 0 and Proc 1 perform loads and stores to these addresses. As discussed in the demo in class, the coherence protocol will result in the following behavior:
(Assume the original values at address X and address Y are 0. Also, below I'll use X loosely to mean the line containing X. Ditto for Y.)
P0 load X:
P0 triggers BusRd for X
P0 loads X (value=0) into S state
P0 receives data (value=0) from its cache
P1 load X:
P1 triggers BusRd for X
P1 loads X (value=0) into S state
P1 receives data (value=0) from its cache
P0 store 1 to X:
P0 triggers BusRdX for X
P1 invalidates X
P0 loads X (value=0) to M state
P0 writes 1 to X
P1 store 10 to X:
P1 triggers BusRdX for X
P0 flushes X, memory now contains value 1 at address X
P0 invalidates X
P1 loads X (value=1) into M state
P1 writes 10 to X
P1 store 25 to X:
P1 writes 25 to X
P0 load X:
P0 triggers BusRd for X
P1 flushes X, memory now contains value 25 at address X
P1 transitions X to S state
P0 loads X (value=25) into S state
P0 receives data (value=25) from its cache
P1 load X:
P1 receives data (value=25) from its cache
P1 store 50 to Y:
P1 triggers BusRdX for Y
P1 loads Y (value=0) into M state
P1 writes 50 to Y
P0 load Y:
P0 triggers BusRd for Y
P1 flushes Y, memory now contains value 50 at address Y
P1 transitions Y to S state
P0 loads Y (value=50) into S state
P0 receives data (value=50) from its cache
This comment was marked helpful 3 times.


The way we pad the variable here only works if our cache line size is 64 bytes. What if we want to write code that will pad properly on any architecture? Is some standard/idiomatic way in C/C++ to pad variables to avoid false sharing?
This comment was marked helpful 0 times.

Well I'm not sure if there's a better way in C/C++ but using the CPUID instruction on Intel CPUs can give you all sorts of information about the cache. I'm sure other architectures have something similar?
This link gives more information about the CPUID instruction. A table at the end of the page lists what may be returned about the cache.
This comment was marked helpful 0 times.

Obviously this is a horrible, hacky way to write code (although maybe it could be an optimization left to a compiler). To me, it seems a nicer way to handle problems like this is to relax our definition of what we require for cache coherence. I would argue that rather than requiring each processor to see the edits in the "actual" order they occurred in, we should simply require that each processor sees the edits in one possible execution order given the program. Therefore, if the program is concurrent, we require synchronization to get the expected behavior in memory. Then for code like this, where we don't need synchronization, we don't need cache coherence either (since each array element is being acted on independently so no processor needs to see any other processor's updates), given we'll need to flush the values at some point later when we need to read them. This doesn't break any abstractions because it makes it so that cache coherence issues are indistinguishable from race conditions (I think, or at least they seem to occur in the same situations). I suppose the (possibly big) issue with this is maybe it's not efficient to do "lazy" flushing on synchronization (you have to know which parts of which cache lines have changed, etc.).
This comment was marked helpful 0 times.

@tomshen
Well it would also work for caches with lines that are smaller than 64 bytes as well.
This comment was marked helpful 0 times.

My question is, however, can we assume that the struct is aligned to 64 bytes in memory? The largest element in the struct is an int (4 bytes), and I thought Intel aligned at minimum to the size of biggest element or at the minimum 8 bytes.
This comment was marked helpful 0 times.

@ycp I believe this was briefly mentioned in lecture by a student, and if I recall correctly we cannot assume that. I'm not sure if an answer was given, but from what I've seen, there are a lot of compiler specific ways to do this. For instance, suitably recent versions of gcc have an 'aligned' attribute that can be used to ensure alignment to some number of bytes. I could not find one single, easy, clean way to do it.
This comment was marked helpful 0 times.

Wouldn't it be better if there were hardware support for not caching an entire line, or remembering only how many of the cached bits actually matter? This would reduce false sharing without wasting memory unnecessarily on padding or forcing hacky workarounds.
This comment was marked helpful 0 times.

If we can't know that the struct will be aligned with the cache lines, then this seems like a waste altogether. You're just wasting memory and not getting the benefit of cache locality. It seems to me that compilers / OS's / hardware should align arrays to start at cache lines automatically. Does anyone know if this is done anywhere, or why it isn't?
@benchoi At that point you're basically just caching bytes, which defeats the whole purpose of using a cache line, which is a deliberate decision made by hardware designers. Correct me if I'm wrong, but I believe the point of using a cache line (instead of just caching individual bytes) is to reduce the amount of memory consumed by the overhead bits (i.e. the dirty and tag bits). It's a compromise between fine-grained memory access and wasting memory with overhead.
This comment was marked helpful 0 times.

C++11 and C11 have standardized ways of doing this.
For example, in C11 there is aligned_alloc(size_t bound, size_t nbytes) which returns an allocation of size nbytes, and this allocation is aligned to a bound-byte boundary.
http://www.drdobbs.com/cpp/cs-new-ease-of-use-and-how-the-language/240001401
This comment was marked helpful 0 times.


I found this site about identifying and eliminated false sharing in your code. It walks you through a pretty good example and gives you several means of combating false sharing after that. It has 5 pages (next page link after the text each page)
http://www.drdobbs.com/parallel/eliminate-false-sharing/217500206?pgno=1
This comment was marked helpful 0 times.

One question on the demo:
When P2 wants to write to a cache line that was written by P1, P1 flushed the line to memory in the demo. Is this what happens instead of directly sending the cache line to P2?
This comment was marked helpful 0 times.

P1 does indeed flush the line to memory. When another processor wants to write to the same cache line P1 had written to, P1 is moved to the invalid state (following the blue dotted line of BusRdX from Modified to Invalid).
See this slide.
This comment was marked helpful 0 times.

In the demo, we were enacting the MSI protocol, which would require the processor sustaining the miss after an invalidation to fetch the data from memory.
The more advanced protocols in modern CPUs do involve cache-to-cache transfers like you suspected.
This comment was marked helpful 0 times.
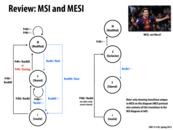

The MSI diagram is symmetrical (each "to" edge has a corresponding "from" edge), but the MESI diagram isn't. In particular, there is no direct M->E or S->E transition.
The M->E transition wouldn't make sense to have because the only two reasons to leave the M state are when someone else plans to read or write. In either case, the first owner wouldn't have exclusive access to the data.
The S->E transition also wouldn't make sense. At the moment you enter the S state, you're guaranteed that someone else is also in the S state (otherwise you would go to the E state). But you don't know if/when the shared owners drop to the I state after an eviction. So to move to the E state, you would have to ask if anyone is still sharing that data. This defeats the whole purpose of the E state though, which is to reduce communication.
This comment was marked helpful 0 times.

In addition, there the advantage of the MESI protocol lies in the common operation of reading some data from memory and then repeatedly reading that data and writing to that data. If our processor is at the exclusive state, no signaling has to be done to move the data into the modify state or read data in the exclusive state. However, in the MSI protocol, reading data and then moving to the modify state will require the processor to send a BusRdx to every other processor even though no other processor will respond.
However, an offset of this is that data loads must be done by sending a signal to the other processors and waiting for a result from those processors. This is in contrast to the MSI protocol where no processor needs to hear responses from other processors after sending a signal.
This comment was marked helpful 1 times.


The probability of a capacity miss can be reduced by enlarging the cache simply because capacity misses occur due to lack of space in the cache. With a conflict miss, too much of the working set maps to the same cache set, resulting in evictions of cache lines even when there is space elsewhere in the cache (in different sets). Increasing cache associativity provides more lines per set, alleviating the conflicts within a set. These two solutions make some sense to me. However, I am not sure I understand how increasing line size decreases cold misses. I was under the impression that cold misses were unavoidable since they just result from the cache being empty. If this is the case, then how can cold misses be decreased with a larger cache line size?
This comment was marked helpful 0 times.

"spatial locality present" is an important caveat there. On a clean cache with 32-byte cache lines, iterating across a 64-byte array will cost you two cold misses. If you make the lines 64-bytes long instead, you'll only get one cold miss. If the data set you're working with isn't contiguous in memory, on the other hand, you can't make the same conclusion.
This comment was marked helpful 0 times.


I think the assumption here is that only the cache line size increases, so the total size of cache remains the same. In this case, either the associativity decrease or the number of sets decrease.
The reason that the miss rate decreases is that since each cache line size increases, for the same amount of data (suppose good locality), each miss would bring more useful data than smaller cache line size. It is also the reason that the true sharing decreases, since there is less coherence traffic.
This comment was marked helpful 0 times.

This might be irrelevant, but what are the "Upgrade" misses (and why do they decrease more on Radix Sort)? Thanks!
This comment was marked helpful 0 times.

@aew: upgrade miss is when a line in the S state is "upgraded" to the M state when the processor wants to write to it. This involves an announcement of the intent to write, but doesn't require data to be fetched from memory since the data in the S state in the cache is valid. This is a small optimization on the basic MSI protocol as we discussed in class. However, notice that my diagram technically says movement from S to M triggers a BusRdX just like movement from I to M. In that lecture, BusRdX meant send the request for exclusive access on the interconnect and read the data from memory. Really all that's necessary is to make sure the exclusive access request is broadcast -- that's the bus upgrade. In fact, it's such an obvious thing to do it was clear from a couple of questions in class that students were assuming this was the case in the MSI protocol, although technically it does not include this optimization.
This comment was marked helpful 1 times.

The reason why we see a larger bar for larger cache line sizes in Radix sort is because the majority of the misses are false sharing misses. Since the cache lines are so large, it even more likely for multiple threads to be accessing the same cache line.
This comment was marked helpful 0 times.

There are a few things I notice about these graphs:
- In all cases, increasing line size decreases cold misses, because each miss brings in a larger amount of data
- It also decreases true sharing misses for the same reason, because there are fewer cache lines to bounce back and forth when two processors share the same data
- It also seems to decrease conflict and capacity misses (although Ocean Sim is the only application that has any), probably because the application will repeatedly use different parts of the larger cache line, rather than continuously dropping and picking up smaller parts of it because a different part was being used
- However, increased cache line size increases false sharing misses, because with a larger line size there is a higher probability that more than one processor will want the data on that cache line
Because of the last point, there is a certain line size that is ideal for most of the applications, and if you go above that false sharing misses increase too much. However, for Ocean Sim, since it has no false sharing misses that is not the case and larger cache lines always result in fewer overall misses.
This comment was marked helpful 0 times.


Question: I am very confused on the implementation of Radix sort from this slide.
Here is my understanding that is possibly wrong: each square represents a number and their color represent the bin it belongs to. Take the first blue square in P2 for example. My question is that how does P2 know to put it at index 5 instead of 4 or some other places in the bin? Does the processors coordinate to agree on which chunk of the bin each processor can write to?
Thanks :D
This comment was marked helpful 0 times.

This confused me for a really long time too, but I think I finally understand it now.
I believe that everything you've written out is correct. As for how the processors know where to put the numbers in the final bin, from what I understand, that process would be similar to how we implemented find_repeats. The entire process would go as follows:
- In parallel, make a thread for each element and find the bin each element should go into. This could very easily be done as a bitmask (
0xFin this case). - In parallel, make a thread for each bin and map each element to 1 if it is in the bin, 0 if it is not. Then, run prefix-sum exclusive scan over these lists of 1's and 0's.
- Given the bin number $b$ and the index $i$ of an element in the overall array, take the scan result for the $b$-th bin and index $i$ of that result will tell you where in that bin to put the element.
This comment was marked helpful 0 times.

Yes, @spilledmilk is correct. To clarify and summarize:
Step 1. Each processor bins the elements it is responsible for. Each processor now has counts for each bin.
Step 2. Aggregate all those counts to get per-processor offsets into each bin.
Step 3. "Scatter" the elements to the correct offsets. Each processor will write a contiguous chunk of offsets into each bin, as illustrated by the arrows on the slide.
If someone wanted to try their hand and some basic pseudocode, that might help others. For low processor counts, it would be quite reasonable to perform the offset calculations serially on one node, and not implement a data-parallel scheme.
This comment was marked helpful 0 times.

I'd like to clarify why false sharing occurs in this example. The figure illustrates how, in each round of the radix sort, each processor will compute the bin in the output array that its input array elements should be moved to (elements assigned to P2 are colored according to their bin). Given the mapping of elements to bins, the algorithm then computes the precise output location each element should be moved to. Each processor then scatters its elements to the appropriate location in the output array (as shown by the arrows in the figure).
By the nature of a stable radix sort, each process P writes its elements that belong to the same bin to a contiguous region of the output array. In this example, P2 never writes more than two consecutive elements to the output, since it is not assigned more than two elements mapping to the same bin. Noe remember that P0, P1, and P3 are also scattering their elements into the output. The result is an access pattern where each processor is scattering data all over memory.
Now recall that to perform a write, a processor must first obtain exclusive access to the cache line containing the address. In the case of radix sort above, many processors might end up writing to the same cache line (since it's likely all processors have elements falling in each bin). This will cause the cache line to bounce all around the machine. There is no inherent communication between the processors in the scatter step of the algorithm, so the extra cache invalidations during the scatter are due to false sharing.
Notice that if the array to sort is very large, each processor is responsible for more data, and it is more likely that each processor will write larger ranges of contiguous elements to the output array. This decreases false sharing by dropping the likelihood multiple processors write to the same line. Conversely, if the number of processors is large, the number of elements per processor decreases, leading again to few contiguous writes per processor, and thus more false sharing.
This comment was marked helpful 0 times.


The bandwidth goes up as cache line increases and it's bad in a sense that we're more likely to be bandwidth-bound.
Reducing cache misses does not always result in reducing data BW.
This comment was marked helpful 0 times.

Slides clearly show us that our cache line size may help latency but may affect bandwidth negatively.
This comment was marked helpful 0 times.

Let me see if I get this: so, in the previous slide, we showed that as cache line size increases, miss rates decrease, with the exception of radix sort. Over here, we see that as cache line size increases, bandwidth skyrockets in all cases except for LU. We can say that LU (and some other cases, to a certain extent) has good spatial locality since increasing the cache line size does not increase the bandwidth, which means that once it loads a cache line in, it will take a long time to miss again.
Now, with other cases, without Radix sort, we saw that miss rates were decreasing. However, the reason why bandwidth increases is that each time we miss, we need to load a big chunk of data from memory (since the cache line is bigger).
With radix sort, we saw that miss rates were increasing, so obviously bandwidth will increase.
If we are bandwidth-bound, then we might get more performance by decreasing the cache size and taking more misses (utilizing more latency). If we are latency-bound, then we might get more performance by increasing the cache size and taking less misses (utilizing more bandwidth).
This comment was marked helpful 0 times.

@taegyunk Its not necessarily true that this will make us more easily bandwidth bound. If we are reading a large data set in, we will definitely end up using the entire cache line (even if it is large). This would mean that the cache line size does not actually matter. This is more of a concern if we are running programs that are reading small amounts of data from many sporadic locations.
This comment was marked helpful 0 times.

What is LU and why is its traffic usage trends so different from the other applications? Also, what exactly is sent over the data bus and address bus?
This comment was marked helpful 0 times.


If you only "use" a small portion of the cache line after pulling in a cache line, then your program has poor spatial locality.
As we could see with Ray Trace/Ocean (on the previous slide), larger cache lines with poor spatial locality caused an increase of bandwidth -- more data has to be pulled in on each miss, and the misses still happen a decent amount due to the poor spatial locality.
Thus, if your program is "bandwidth limited" and had poor spatial locality, then having a large cache line would be pretty bad.
This comment was marked helpful 2 times.

Nice!
This comment was marked helpful 0 times.

If the programmer of this cache makes a mistake in the tradeoff between interconnect traffic and fewer misses, could this not be the source of a security vulnerability? I was reading on wikipedia about cache poisoning attacks where the attacker causes irrelevant data to be cached, which in this case would mean there would be much more traffic trying to retrieve the correct data, possibly causing a dramatic slowdown in the program or corrupting the cache.
This comment was marked helpful 0 times.

Is there a way for a program to determine the cache line size of the machine it is operating on? If it could I suppose to could optimize its data structure layout to obtain more performance
This comment was marked helpful 0 times.

@Q_Q Here is a possible solution. The nice thing is that is works on Linux, Windows and OSX operating systems.
This comment was marked helpful 1 times.


Wouldn't there be a problem if a processor in SC wants to read data, but another processor in SM is writing to the cache line but has not yet updated SC?
This comment was marked helpful 0 times.

@jinghuan: I think the "after some certain time" constraint in last lecture is also needed here.
This comment was marked helpful 0 times.

@jinghuan: Good question. Imagine P0 has the line in the SC state and P1 has the line in the SM state. Lets say that X is 0. Let's say P1 writes 10 to X in clock t. P0 reads X in clock t and observes 0. P1's update gets to P0 in clock t+1. P0 read X again in clock t+1 and observes 10. Say P1 writes 20 to X in clock t+1. This update gets to P0 in t+2, and P0 observes 20 in t+2.
This system is coherent, since:
- All of P1's write occur in program order -- just assume this is the case here --
- It obeys write propagation (the write eventually gets to P0)
- it obeys write serialization. Both processors agree that the following sequence of writes occurred in the following order. X = 0, then X = 10, then X = 20
This comment was marked helpful 0 times.


What does update rate % exactly stand for in this case?
This comment was marked helpful 0 times.

My best guess would be the percentage of memory writes that cause an invalidation/update when those programs are run.
This comment was marked helpful 0 times.

@ycp is probably correct. This graph mainly shows that the update policy enforces a lot of traffic. In this case the traffic isn't necessary. The invalidate policy is a bit lazier, the only time a processor (or rather, a cache) does work is when it needs to. I think for the more general case this is probably preferable. As we can see, both AMD and Intel would probably say the same thing. I think generally this is true because parallel programming techniques would likely minimize the amount cache line sharing.
This comment was marked helpful 0 times.


A is the more recently used item by the processor and is therefore more recently used in L1. (B is therefore less recently used in L1 and will be evicted from L1.) For the very same reason, A will actually be less recently used in L2 and will therefore be evicted from L2.
This comment was marked helpful 0 times.

In other words, at the time that a processor needs an item from memory, both L1 and L2 will have it in their caches once it is retrieved from memory. However, because the access patterns differ in each level, the eviction policy might evict from one cache and not another.
This comment was marked helpful 0 times.
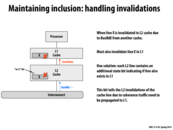

Question: Can someone describe a sequence of operations that could cause coherence to be violated if the L2 cache did not take special care to invalidate the appropriate line in the L1 upon receiving a BusRdX message over the interconnect?
This comment was marked helpful 0 times.

Let's say that P0 has X in its L1 and L2 cache, in the shared state. And then P1 broadcasts its desire for exclusive access for a write, by shouting BusRdX on the interconnect. If L2 does not invalidate the L1, then the following can happen. P1 will now think that it has exclusive access, and thus it can modify it without sending any messages on the interconnect. Likewise, since P0 has X in shared state, P0 can read the value of X without sending any messages on the interconnect. This means that any updates made to X by P1 is not visible to P0.
This comment was marked helpful 0 times.


So to solve these inclusion problem, the solution is to add bits to maintain the line state. My question is though, wouldn't the increase in bits pose a significant overhead for the already small L2 cache?
This comment was marked helpful 0 times.

@sss It does add overhead, but considering that a cache line holds holds 64 bytes, or 512 bits, the few extra metadata bits aren't much to worry about, in this case, less than half a percent.
This comment was marked helpful 0 times.


In general, I would expect that this could be extremely inefficient if the amount of data that is shared between caches is modified by different processors, in a sense "thrashing" the cache. This, in my understanding is the idea behind false sharing in this case. The bullet point above about interconnect traffic is also concerning since each processor could potentially be "shouting", thus causing a lot of overhead.
This comment was marked helpful 0 times.

pwei - this is why the bullet point is labeled "workload-driven evaluation", there are a lot of potential increased costs but the question is will they outweigh the savings for your specific workload? Increasing the cache line size can have the problems you're mentioning, but it also reduces cold/capacity/trueshare misses and we saw in many of the graphs in this lecture that it reduced overall cache misses. The only real way to decide whether it's worth it is to think about how much of your program's runtime is taken up by cold/capacity/trueshare misses and how much false sharing would increase if you increased the cache size.
This comment was marked helpful 0 times.









I'm beginning to feel that these aren't real quotes...
This comment was marked helpful 0 times.