

Can someone describe why this kernel code deadlocks?
This comment was marked helpful 0 times.

If a group of threads have to run to completion before the next group begins, then there will be a deadlock, because the first group will never complete due to __syncthreads() not returning. __syncthreads() will not return because the other threads will never get to run.
This comment was marked helpful 2 times.

Specifically, there is no preemption of CUDA threads. Once a CUDA thread is assigned an execution slot on the hardware, there is no mechanism to relinquish the slot until the thread terminates.
This comment was marked helpful 2 times.

@smklein I think it's not necessarily that the code produces a logical deadlock, but that certain implementations will result in a deadlock (if the threads are not processed concurrently).
This comment was marked helpful 0 times.

I think the deadlock hazard here is if the first group of threads that parallel executed in kernel does not have the threadIdx.x smaller than two (which is weird to me), then all threads are waiting for the assignment of support array for threadIdx.x < 2 case, which will never happen unless this group of threads finished executing. That's why there is a dependency between threads in a block.
This comment was marked helpful 0 times.

But then I have a question about: even though the threads are divided to two groups to execute, isn't that for each of the group there would be at least a thread whose idx.x must be less than 2? Therefore there should not be a deadlock at all. I would feel if the if (threadidx.x < 2) is changed to (index < 2), there would be a potential deadlock due to thread dependencies...
This comment was marked helpful 1 times.

Even, I am not too clear as to why the above code would deadlock. This is because the only assignments happening before the __syncthreads() are using the input array which is never modified by any other thread block so I am not able to exactly figure out why there would be a dependency leading to a deadlock.
This comment was marked helpful 0 times.

I don't think this code deadlocks - the code here illustrates the case where there is no deadlock because __syncthreads() is between threads in the same block, and all the threads in a block run concurrently. So, each thread in the block has the opportunity to run and reach the barrier.
This comment was marked helpful 1 times.


What are swizzle and vote? Are they anything we might find useful programming in CUDA?
This comment was marked helpful 0 times.

Just to confirm:
Threads in a block are run concurrently and so they can be synchronized. However, thread blocks are like ISPC tasks and are run independently of each other. Is that right?
This comment was marked helpful 0 times.

@ycp: I like your analogy.
I would prefer to say "Threads in a thread block are run concurrently because CUDA's abstractions allow these threads to communicate and synchronize in ways that require concurrent execution."
This comment was marked helpful 0 times.

Vote is use to perform reduction operations and subsequently broadcast the result to all threads.
Swizzle is used to create other-sized vectors out of four-vectors, because all registers on the GPU are four-vectors. This is used since other instructions may not take four-vectors as arguments.
This comment was marked helpful 0 times.
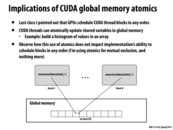

In functionality atomicSum is the same as if you used a lock, but what is the difference in latency?
This comment was marked helpful 0 times.

Yes. You can think of atomicAdd to operate like this.
void atomicAdd(int* addr, int value) {
lock(myLockForAddr);
*addr+=value;
unlock(myLockForAddr);
}
Of course, you wouldn't actually have a lock per memory address, that would be crazy! So atomicAdd is typically a primitive that has direct hardware support. (e.g., an atomicAdd instruction)
This comment was marked helpful 0 times.


Could someone explain why this would deadlock if performed in reverse order? Why wouldn't block 0 run to completion? Are blocks executed to completion before another block can be run?
This comment was marked helpful 0 times.

If you run the blocks sequentially in reverse order without context-switching, then block N would never terminate (as it waits for block 0 to set the flag).
This comment was marked helpful 1 times.

Notice the assumption here is that it is a single core GPU for one block per core, so the core can only run one block at a time. In this case, if block N runs first, then it cannot jump out of the while loop.
This comment was marked helpful 4 times.


Atomic operations cause an overhead, I'm guessing, because the variable needs to be surrounded by some sort of lock. How would a programmer know when this is worth it? Doesn't that require some pretty specific understanding of the chips implementation of different operations?
This comment was marked helpful 0 times.

Atomic operations are an abstraction -- instead needing to know when or where to use a lock, the programmer simply declares that an operation needs to happen atomically. This is assumed to cause a little overhead, simply because of whatever the implementation needs to do to ensure atomicity, but I don't see why the programmer needs to understand the implementation.
If a programmer believes that an algorithm with modification of shared memory is the most appropriate, then they will probably need to use atomic operations. If any extra overhead in that respect is unacceptable, then they will need to rewrite their algorithm to avoid needing atomic operations.
This comment was marked helpful 0 times.

I am wondering why this mechanism is useful? At the last row, it would launch most number of blocks, but which block is working depends on which block first reach the atomic operation. Later blocks would not run if they come to the atomic operation late, and N is not big enough.
This comment was marked helpful 0 times.

@yanzhan2 The benefit is to save block scheduling/switch overhead as well as balancing workload. Notice the while loop in the convolve kernel. The idea is to launch just enough thread blocks to keep all gpu cores busy and each block pulls work from a shared work queue (workCounter). This idea is similar to what ispc task is doing as opposed to launching lots of pthreads.
This comment was marked helpful 0 times.

Expanding on the balancing workload point, I believe this technique is mostly used as a part of Dynamic Assignment, which, as that lecture slide describes, is mostly useful for when "the execution time of tasks, or the total number of tasks, is unpredictable".
Additionally, about @yanzhan2's last point, usually this technique would be used when the amount of work is much greater than the number of total threads so that each thread would do at least a couple of operations before it exits.
This comment was marked helpful 0 times.

Another way to say things is that atomic operations, by definition, require serialization. Only one thread can be executing an atomic operation on a specific address at the same time. If many threads wish to do perform an atomic operation on the same address simultaneously, all of these operations must be serialized.
This comment was marked helpful 0 times.

Since atomic operations are supported by hardware, instead of insanely add a mutex lock to each atomic operation, can I assume that this overhead is actually not very prominent? When having algorithms that requires serialization, is the atomic operation would be best to consider first? Is there any better way in general that is better than using atomic operations?
This comment was marked helpful 0 times.

Atomic operations are very costly. They still need to ensure mutual exclusion, therefore in a multi processor system this is going to incur similar costs to that of a lock. However these costs are reduced slightly because atomic operations are generally highly optimized in the hardware.
This comment was marked helpful 0 times.

Suppose we were to have N threads running on separate cores all trying to add atomically to a shared variable. If atomic operations are supported in hardware and don't in fact involve an additional lock, and these cores all happen to share their highest level cache, would it be reasonable to assume that this N-threaded program would be no slower than a sequential program adding N times? Or is there an additional penalty for using atomic operations beyond their inherently sequential nature and the risk of false sharing?
This comment was marked helpful 0 times.

For GPU, a thread block runs on a single core, and thread blocks are independent with each other, so I guess there won't be situations in which different CUDA threads on different GPU cores trying to update a shared variable.
This comment was marked helpful 0 times.


Question: Is there explicit parallelism in this code? (Does the programming model dictate any of the described logic must run in parallel?)
This comment was marked helpful 0 times.

@kayvonf If I'm recalling this correctly then this was written in Kayvon's mystery language. In which case, the for_all body was written with the intention of being parallel, but whether it actually is depends on the implementation. Unless there was some explicit assignment and/or mapping to a thread, core, etc. I wouldn't say that this code must run in parallel.
This comment was marked helpful 2 times.

I agree with @bxb, the for_all indicates to the compiler that each iteration can be performed in parallel, but does not dictate that it must be run in parallel. So there is not explicit parallelism, just the potential to be parallelized, which depends on the implementation.
This comment was marked helpful 0 times.


In which category would we put frameworks like Hadoop?
This comment was marked helpful 0 times.

I think of Hadoop as closest to a data-parallel model: you specify some map and reduce operation that should be applied to all of the data in your dataset, and the framework handles the scheduling and communication.
This comment was marked helpful 0 times.

I agree.
This comment was marked helpful 0 times.

In addition, Hadoop is designed to run on a cluster of machines that does not share any disk or memory space. This design choice allows Hadoop to run on out of box commodity hardwares. Conceptually, Hadoop's abstraction is closer to data-parallel model, but Hadoop is implemented a little differently from the data-parallel described here. If you wish to explore, you can read about how MapReduce is implemented in Google's paper.
This comment was marked helpful 0 times.
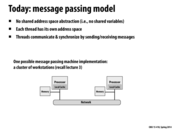

I watched the lecture online, and I didn't see an answer to this question: When is it useful/practical to use a message passing model?
I understand that having no shared address space can be useful for avoiding having two threads update the same variable out of order, but what are some particular cases when the message passing model is better than others that do have a shared address space?
This comment was marked helpful 0 times.

This page here is pretty good at explaining the details:
Just to summarize, here are some reasons why you'd want to use a message-passing model:
- Your hardware system can be simpler (eg NUMA). If all components of the
system don't need share the same memory space, it allows you to 'distribute' your memory addresses substantially. Distributed systems, by definition, would use message-passing models for this reason. - Synchronization is a bit cleaner in a message-passing model. You don't need to use semaphores and locks in a message-passing model; you just need mechanisms to pass data and messages across components.
Of course, there is the overhead of constructing/sending/receiving messages in such a system. However, message-passing makes sense in a variety of contexts. For instance, an operating system is essentially built on message-passing, via interrupts, signals, I/O, etc.
This comment was marked helpful 1 times.

I feel that another flaw in the message passing model (more for distributed systems rather than at the OS level) is that it seems like a process or task assigned to manage the sending and receiving of messages from task to task.
The problem that I see is that if one task depends on a message sent from another task to start processing, and the message passing manager is not currently running, there could be deadlocks from the lack of message passing capability.
Overall, I think OS message passing has better utility because of how signals are built into the system but message systems above the OS layers need more micromanaging about message handlers and receivers.
This comment was marked helpful 0 times.


I'm not sure how efficient the message passing model would be for the grid problem as compared to the shared address space model. Since the different parts of the array are located in private address spaces, I'm assuming it would require more overhead to send/receive the data necessary to compute rows compared to when the array is stored in an address space accessible to all threads. Does this seem correct?
This comment was marked helpful 0 times.

I think you're probably right about that, but we still have to pay the synchronization costs, and we have to worry about cache coherency. It's also possible that restricting the memory to be for a single core allows the hardware people to make it faster for that core (a NUMA-style thing), while shared memory would be slow for everybody. I'm not sure how these factors balance out.
This comment was marked helpful 0 times.


C++ (or pseudocode in this case) can be kind of ugly, so it's nice to look at how channels/message-passing is implemented in other languages. In particular, I find Go and Rust to have quite lovely support for this sort of things.
Channels in Go:
channel := make(chan int)
go func() {
for {
fmt.Println(<-channel)
}
}()
i := 0
for {
channel <- i
i += 1
}
Channels in Rust:
let (port, chan) = Chan::new();
do spawn {
while (true) {
println!("{:d}", port.recv())
}
}
let mut i = 0;
while (true) {
i = i + 1;
chan.send(i)
}
This comment was marked helpful 4 times.

My understanding of this code is that each processor iterates over the part of the array that they are assigned to, and there is some communication between processors so that each processor sends its top row to the processor above it and its bottoms row to the processor below it, and some more computation is performed.
(I'm a little bit fuzzy on what happens while the processors are exchanging rows. I know they become dead-locked while waiting for a response, but I'm not 100% sure why they're exchanging rows in the first place)
Then eventually every processor sends their results to Processor 0, which adds up all the results and sends a message to all the other processors saying that the computation is finished.
Because information is only shared through sends and receives, there are implicit locks around the parts of the array each processor is working on.
If anyone wants to fill in anything I'm missing, I'd appreciate it.
This comment was marked helpful 0 times.

The reason they need to send rows around is that the value of each point in the grid is a function of its four neighboring points (a weighted average maybe, or else something more complicated). If we're dividing work up by rows, then the last row a processor is responsible for computing depends on the values of the row after it, so the processor has to get the values of the row after it from the next processor in line. That's where the message-passing comes in.
This comment was marked helpful 1 times.

@mpile13: This illustration on slide 17 might be helpful to understanding why the previous and next rows are communicated.
Question: Why is the program sending entire rows in a single message, and not sending one message per grid element?
This comment was marked helpful 0 times.

Maybe the program sends entire rows because that minimizes the amount of overhead caused by sending a message? Or is there something deeper than that?
This comment was marked helpful 0 times.

Sending a message, as we reviewed earlier is expensive since it requires copying information over from the send buf to the network buffer and again to the receive buf. Not to mention that if it's blocking, we also have latency as a result. So we want to maximize the information we can send as a message.
This comment was marked helpful 0 times.


Why: Say the two machines/threads/etc (I'll say threads here) for a pair of adjacent blocks of rows each call SEND to each other at the same time. Each SEND would then wait for the other thread to call RECEIVE, which in turn cannot happen because it is waiting for SEND to complete. So neither thread can call RECEIVE to un-block the other thread. So there is a chance of this deadlocking.
Fix: One simple way to fix this would be to impose an ordering on communication between threads. For example, perhaps each thread must wait for the thread "above" it (the thread responsible for the blocks further along the Y axis of the grid) to send it a message, by RECEIVEing first. The top thread would not need to wait for any others, so eventually this linear chain of dependencies would complete. We can then repeat the process in the opposite direction.
This has the unfortunate side effect of serializing all communication, although the computation is still parallel. We could probably design more complex schemes that would reduce the serialization.
This comment was marked helpful 0 times.

Another fix suggested in class was to have all of the threads with even PIDs wait to RECEIVE from the ones with odd PIDs to SEND, and then switch around so that odd PIDs wait for even ones. This parallelizes the communication, instead of doing it serially.
This comment was marked helpful 0 times.


Is there not a problem here with the fact that the sender does not guarantee the message/data has sent and the receiver does not acknowledge that it has gotten the message/data? How is the programmer supposed to maintain information integrity in this kind of scenario? Is this type of messaging therefore meant for situations where the message/data is continuously updated so it does not matter if some data is lost?
This comment was marked helpful 0 times.

I suspect that in this setup the underlying communication protocol can independently guarantee message delivery. When the sender sends, it doesn't have to manually check for an ACK because it's guaranteed that the message will be delivered. On the other side, the receiver doesn't have to manually send an ACK because the sender doesn't need this explicit acknowledgement.
If however the communication protocol can't guarantee that messages will be delivered successfully, then I think it would be possible for the program to become non-deterministic, exhibiting varying behavior depending on which messages were lost.
This comment was marked helpful 1 times.

To me blocking send/receive seems to have very limited usage, since it does not return until it makes sure the data is completely sent or received. Thus, it seems like it would be useful only when it is specified which thread will be sending data and which data will be receiving data.
However, since blocking ensures that data is indeed sent/received, I believe that this could be possibly used for safety of data delivery.
This comment was marked helpful 0 times.

Whether or not you want to use blocking send/recv probably depends on how reliable the specific message protocol is, how fast it is for your usage, and how important individual messages are.
In most cases, waiting for a message to send is probably undesirable. If your processes are on cores geographically separated, latency explodes, and you simply can't wait for the data to travel all the way there and an ack to travel all the way back before continuing execution -- it would probably be faster just to send the message twice just in case. On the other extreme, if your processes are on the same computer, you can probably be reasonably confident that the OS is passing messages successfully, so blocking is unnecessary.
This comment was marked helpful 0 times.


How does SENDPROBE work? Is it simply a lock to data? If the SENDPROBE is not returned and thread is willing to modify 'foo' then isn't the thread is still blocked?
This comment was marked helpful 0 times.

'SENDPROBE(h)' is simply a call that returns tells the calling program if the message referred to be the handle h has been successfully sent by the messaging system. If SENDPROBE indicates the message has not been sent, then the application should not modify the contents of foo.
Logically, the following pseudocode that uses a non-blocking send followed by a SENDPROBE is equivalent to a blocking send.
h = NON_BLOCKING_SEND(foo);
while (!SENDPROBE(h)) {}
This comment was marked helpful 1 times.

So why exactly do we need to even check that the message has been sent? Once we have copied the data into the network buffer, we should be free to modify foo as we wish since there is a copy of foo in the network buffer and it is now the responsibility of the network to transfer the information.
The only exception I can think of is that for some reason, the network buffer might need to read from foo again - though I can't think of why this would ever need to happen - and if foo is modified, then we have a problem.
This comment was marked helpful 0 times.

@rokhinip: How do you know that the data has been sent? That's the purpose of SENDPROBE. (Technically, it is even more conservative and it returns true if the message has been received.)
This comment was marked helpful 0 times.

I suppose we can't quite assume that the network protocol we are using should guarantee that foo has been sent then?
This comment was marked helpful 0 times.

"Non-blocking" and "asynchronous" mean the same thing to me, so to disambiguate: here, the SEND call is asynchronous and returns immediately; the RECV call is non-blocking and returns immediately (and requires checks to guarantee the data has actually been received.)
On the previous slide, "blocking asynchronous" again means that the SEND call returns immediately but that the RECV call blocks.
This comment was marked helpful 0 times.

It seems to me that there is a slight difference between blocking asynchronous and non-blocking asynchronous, in that blocking asynchronous will wait for the data to be transferred into the network buffers but will not wait for the acknowledgements. Non-blocking asynchronous waits for neither.
This comment was marked helpful 0 times.


As we all already have solved in assignment 1, the blocked assignment for Mandelbrot Set resulted in imbalance of workload. However, the interleaved assignment solved it because each consecutive row didn't much differ in the amount of computation.
This comment was marked helpful 0 times.

Question: Here I claim that the static assignment has "essentially zero" runtime overhead. What did it mean by this? When I say overhead, what is the baseline that I am comparing to? In slide 32 introduce the idea of dynamic assignment. What is the "overhead" of performing a dynamic assignment of work to worker threads in that example?
This comment was marked helpful 0 times.

@kayvonf: Presumably, in order for each worker unit (eg a pthread in the case of ISPC tasks) to know what chunk of work it needs to work on next, it would need to query some kind of global queue (or in the case of slide 34, it needs to read from count and atomically increment it). Maintaining this data structure which is distributing the work dynamically could lead to overhead costs.
This comment was marked helpful 0 times.

@kayvonf: the "overhead" of dynamic assignment is more broadly any logic the program needs to run to intelligently decompose the problem and assign tasks. In the above example, there is essentially zero overhead because assigning a row to a processor requires a single modulus operation. But if we instead dynamically decomposed work using a complex heuristic function and maintained tasks (as @rokhinip mentioned) in a queue, that potentially introduces a ton of overhead.
This comment was marked helpful 0 times.


If anyone's interested in the first example: Barnes-Hut
edit: I noob, how 2 link?
This comment was marked helpful 0 times.

@kkz you can find how to link in here
This comment was marked helpful 0 times.

lol, didn't know you could directly enter HTML code
This comment was marked helpful 0 times.

And the course notes on Markdown are here.
This comment was marked helpful 0 times.


I failed to see why the program on the right is a parallel one, isn't it just a sequential program as written? Where is the multiple threads launched?
This comment was marked helpful 0 times.

@ruoyul It looks sequential, but since it is labelled as SPMD, the implementation of this language must have parallel constructs to it not explicitly seen in this example.
This comment was marked helpful 0 times.

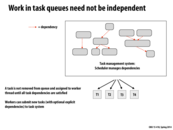
The code on this thread is very similar to the code on slide 9 for CUDA persistent threads. In both cases, the program has some pool of "things to do", and each worker finds the next thing to do off the list. On slide 9, the purpose was to circumvent CUDA's internal scheduling mechanism, and to ensure that synchronization between blocks won't result in deadlock.
The more general use of dynamic scheduling is for dealing with scenarios where the size of the subtasks is unpredictable (e.g. very data-dependent), and it is impossible to determine a good allocation scheme a priori.
This comment was marked helpful 0 times.
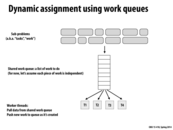

Another interesting queueing problem that can be mitigated with this strategy is the department store checkout queue or telephone operator queue. In the sense of work, each customer waiting brings an independent but potentially different amount of work. And by using a single queue for the system, whenever any operator or clerk gets blocked by a large amount of work, other operators or clerk can still receive work that may have been allocated to that blocked operator in a multi queue system.
This comment was marked helpful 0 times.

As I understand it, ISPC implements the foreach construct by SIMD. Hence, work cannot be assigned dynamically to individual instances. However, it may be possible to achieve dynamic assignment with tasks. For example, with the prime example, we can launch N tasks that only works one number, and when that task is finished, ISPC will schedule another task on the CPU (can someone elaborate?).
On the other hand, CUDA already has a way to achieve dynamic assignment with blocks. When a block finishes, CUDA pulls out another block, and reuses context of the finished block to execute the new one.
This comment was marked helpful 0 times.

I believe ISPC actually uses dynamic assignment to assign workers/pthreads to tasks. When you specify the number of tasks to launch in ISPC, you are specifying the granularity of each task aka the chunk of work to be executed by each worker.
This comment was marked helpful 0 times.

Is the queue just a FIFO queue? How does this help to balance the workload across threads then?
For example, we have tasks 1 through 8, and 4 threads, p1 to p4. The best balance happens when 1,2 go to p1, 3,4 go to p2, 5,6 go to p3, and 7,8 go to p4. In this case, if the queue was a FIFO queue, at runtime, the program would have to send 1,3,5,7,2,4,6,8 to the queue in order to balance workloads in a equal manner.
Does the program calculate all this before placing tasks into the queue, or do threads just pull tasks from the queue according to how much more work they need to become balanced with the other threads?
This comment was marked helpful 0 times.


The difference between this slides and next slides is that: Every thread will be assigned more work to do every time it get access to the critical section(black). The contentions are reduced and each thread could be more efficient with "real" work, instead of frequently asking for access to critical section.
This comment was marked helpful 0 times.


In this example, each thread is being assigned GRANULARITY units of work on each access to the critical section. In this way, we're reducing the amount of contention that the threads have for that critical section. This is different from the previous slide where each thread was assigned one piece of work on each access to the critical section.
This comment was marked helpful 0 times.

Exactly! The key detail here is the ratio of the time spent in the critical section to the time spent doing the work that is assigned.
If the time in the critical section is short (for example, if the lock is a very high performance spin lock) or if the cost of doing the actual work is high (e.g., a very large number), then you may not need to worry about the optimization on this slide.
Another way to think about this slide is that the code has redefined the notion of a "piece of work" to be computing primality of a block of GRANULARITY numbers, not just one number.
This comment was marked helpful 0 times.


This seems to have been the most important guideline for program 3, part 2 on assignment 1. Even though the machines only had 4 processors, dividing the work into 4 tasks didn't even come close to the maximum speedup possible. Personally, I started getting the maximum speedup I could once I increased to 80 tasks. This happened because as the tasks got smaller, there was more leeway with how they could be distributed to balance the workload.
However, one thing that confused me as I did that problem on assignment 1 is that the speedup didn't decrease even as I increased to 800 tasks (the maximum since the image had 800 rows). It seemed to me like the benefit of finer granularity would fall off as more tasks were added. I guess this was just an example of the benefits of workload balancing canceling out the problems with overhead?
This comment was marked helpful 0 times.

@jmnash I agree; in this case, the overhead of launching another ispc task was more than covered up by the fact that each task had a significant amount of work (calculating values for width elements, which in this case was 1200).
The reason why we didn't see an increase in performance was simply because there weren't enough cores to run those tasks simultaneously. However, it did significantly even out the work distribution, as no core got 'overworked' by having the misfortune of being assigned most of the work (which is what happens when you only have 4 tasks; the middle two rows far outweigh the other rows in terms of work required).
However, something very different happens when you use an image with a much smaller width. I tried running the program with width = 4 (same height = 800). Here are my results:
- 4 tasks: 1.75x
- 8 tasks: 1.92x
- 16 tasks: 2.75x
- 32 tasks: 3.07x
- 50 tasks: 3.10x
- 100 tasks: 2.36x
- 200 tasks: 2.33x
- 400 tasks: 2.28x
There is actually a dip in performance when you increase the number of tasks; this is because the tasks are now doing far less work, so the overhead cost of launching a task is now significant.
This comment was marked helpful 3 times.

Excellent post @arjunh.
This comment was marked helpful 0 times.


Just wanted to point out that this idea was crucial in deciding how to assign work in the mandelbrot-set problem on assignment 1 (namely program 3). The idea was to create many small tasks; this way, each processor would receive a roughly equal amount of work.
For example, suppose that we have two tasks, T1 and T2 and two processors, P1 and P2. T1 takes longer to execute than T2 by a substantial amount. If we were to assign T1 and T2 to processors, then one processor would get a significantly larger amount of work than the other. However, if we split the tasks T1 and T2 into roughly even parts, into T1A, T1B and T2A, T2B,then it is almost guaranteed that the work-load on the two processors will be about the same.
In this case, the synchronization overhead/cost of launching an extra task is insignificant, as each tasks is assigned a substantial amount of work.
This comment was marked helpful 1 times.

I would like to ask, talking about workload balance, is there a universal methodology to do this balancing? Like any models or like design patterns in software engineering? Or this is more like an tradeoff made depending on experience?
This comment was marked helpful 0 times.

It depends on whether we know how long each task is going to take. Sometimes it might be deterministic, but sometimes not easily predicted (e.g. if each task is to mine some piece of information). In the latter case it may be helpful to model the distribution of times taken. If we don't know the distribution, it may be helpful to use a randomized algorithm for scheduling.
This comment was marked helpful 0 times.


This problem reminds me of what I have learnt in greedy algorithms, minimizing the entire completion time is a NP-complete problem. It's another way of phrasing bin-packing problem, which is used in memory allocation strategy.
This comment was marked helpful 0 times.

That's a good point, but I bet the cases where it's hard don't come up in practice, so that it's possible to write something that performs near-optimal. Can anyone think of a realistic situation where not only is it hard to come up with a good balance of work; it's hard to even come up with a good approximation?
This comment was marked helpful 0 times.

I am curious if there exists a polynomial time algorithm for finding within 2x of optimal for completion time, similar to how we could find within 2x of optimal for TSP using MST in 451. Or if anyone actually knows a reduction from minimizing completion time to TSP.
@mchoquet I believe that if you divide any workload up into small enough tasks, then you'll have a high probability of meeting your optimal work balance or at least within some reasonable approximation. You would need relatively few inherently sequential tasks that you have no way of predicting the approximate workload. I don't think this would be a very common problem, since there are not many tasks that are completely inherently sequential and large enough to cause workbalance complications and impossible to predict their approximate run time.
This comment was marked helpful 0 times.

I think a more useful area to look if you wanted to convert minimizing completion time to a well-studied graph problem would be graph coloring algorithms, since scheduling is very similar to coloring a graph (colors are the processors, jobs are the nodes, and whatever restrictions are placed on the jobs are the edges)
This comment was marked helpful 0 times.

I think here we are mostly just thinking of independent tasks, so the scheduling problem related to graph coloring is a little different (where edges indicate dependencies between jobs). It does, however, bring up the point of how much more complex balancing might be if we also had these restrictions. I know that finding even a constant factor approximation for graph coloring is NP-hard - not sure about bin-packing though.
This comment was marked helpful 0 times.
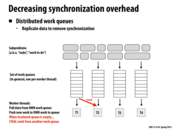

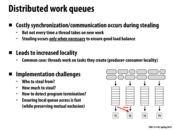
So what is the purpose of having work queues? From the previous slides it would seem that as long as you take the longest task from the pool, you will end up with an optimal (I believe) distribution of work. This whole idea of "stealing" from another queue does make sense given the work queues, but it seems similar to just taking another task from the pool of tasks.
This comment was marked helpful 0 times.

@pwei: I may be off base, but I think it's to minimize the communication between threads. If all the threads are pulling their tasks from the same priority queue, then there will have to be a mutex keeping them from grabbing the same task (unless "pop" is atomic, but in either case accessing the queue can only be done in serial, whereas each thread accessing its own queue can be done in parallel). This could be especially important if there is a chunk of tasks with similar work, in which case threads may all want a new task at the same time.
This comment was marked helpful 1 times.

I'd agree with rbcarlso, and also add that sometimes this is useful if you have a NUMA architecture or a distributed system. In those cases communication time can be just as big a deal as contention, and keeping the relevant data close to the processors is important.
This comment was marked helpful 0 times.





















As a quick recap, an NVIDIA "warp" is comparable to an Intel "hardware-thread", or an ISPC "gang", where an instruction stream is shared.
This comment was marked helpful 0 times.
Further similarity between the ISPC "gangs" and NVIDIA "warps" is that they are strictly SIMD. Each warp can only be executing a single instruction (ignoring ILP) and if a branch occurs, the warp is split into active and inactive threads (active/inactive lanes in ISPC). An important difference between "gangs" and "warps" however is that while the user must manage which lanes are active in SSE/AVX in software, the hardware manages thread activity on NVIDIA GPUs thus this property is only relevent to efficiency and not correctness.
This comment was marked helpful 0 times.
@tchitten: "an important difference" --> "an important implementation difference."
This comment was marked helpful 0 times.
Hi, I am a little confused as to why we can choose only upto 4 runnable warps at any time. This is because I see 32*6 ALU units/6 warps that can run at any time. So shouldn't we able to choose 6 out of the 64 ?
This comment was marked helpful 0 times.
@pradeep. Good question. The answer is simple. That's what this particular NVIDIA chip does! It has been designed to have the capability to choose up to four runnable warps, and up to two independent instructions per each of those warps. NVIDIA architects must have concluded that this was a reasonable amount of decode/dispatch capability for keeping the execution resources busy for the workloads they cared about most.
This comment was marked helpful 0 times.
Yeah that mostly clears it up, but I am still a little hazy as to why the NVIDIA designers would put an extra 32 * 2 ALU's (since we are utilizing only 4 * 32 out of the 6*32 in this chip). Is it there for fault tolerance or may be like for work distribution so that you don't go to the same set of 4 warps again and again and choose another set of 4.
This comment was marked helpful 0 times.
@pradeep. To clarify. The chip has the ability to run 6 instructions (4 arithmetic, 2 load/store), and the capability to find up to 8. So in this sense, it's the opposite of what you mentioned. In an ideal scenario, the chip can decode more than it can run.
This comment was marked helpful 1 times.
@pradeep Keep in mind that there are also two groups of special purpose units and that a warp selector can run two instructions at a time.
This comment was marked helpful 1 times.
@kayvonf I am not sure if I understand what you mean by "two independent instructions per each of those warp"?
This comment was marked helpful 0 times.
@shanbam in lecture 1 we talked about the idea of instruction-level-parallelism, which is that if the processor sees that two nearby instructions (maybe addl x 5 and addl x 3) that are independent, it can execute them in the same clock cycle. That's why the 4 warp selectors on the chip above each have 2 instruction fetchers; they can run 2 instructions at once if those instructions are independent. My interpetation of the above picture was that if among the 8 instructions selected to be run in a single clock cycle, 1 is `special math', 1 is load/store, and 6 are normal math, then all 8 batches of 32-wide SIMD units can be used at once.
This comment was marked helpful 3 times.
@mchoquet. Very nicely said.
This comment was marked helpful 0 times.
For GTX680, is it correct that a warp consists of 32 number of threads? and each thread is basically mapped to each one of 32 shared units?
This comment was marked helpful 0 times.
The max warp size is dependent on the the SIMD lane size. So for GTX680 the warp size is 32. And yes, each cuda thread is mapped to a SIMD unit in the SIMD "block" assigned to the warp.
This comment was marked helpful 0 times.
All the threads in one block will be done in the same core. This core has the shared memory and that's why shared memory can make the program so much faster. Another thing we found in doing the homework is that we don't need to manually free space in the shared memory. When the block has finished, CUDA will automatically free those spaces.
This comment was marked helpful 0 times.