

At first it might seem like latency and bandwidth are directly related to cost, for example that high latency always means a high cost, or a low bandwidth always means a high cost. However, this is not always correct.
One example where there can be high latency, but low cost, is if we employ latency/stall hiding as described in lecture 2. On slide 47 in particular, it shows an example where one core is given 4 threads, and every time a thread hits a stall because it has to go out to memory (which has high latency), it switches context to a different thread. The total time for the operations is slightly longer than if there had been no stalls at all (which reflects that going to memory did have some cost), but it is significantly less than if there had been no context-switching. This shows that although the latency for each memory access was high, the total cost for all of them was relatively low.
This comment was marked helpful 0 times.

This greatly depends on your definition of "cost". If you define it as time spent on finishing all the jobs, then the cost is smaller because throughput is increased. However, if you define your cost as time spent on finishing this specific job, your cost has actually increased because of the thread scheduling and context switching. So it really depends on the definition of "cost".
This comment was marked helpful 0 times.

At first i was confused by the terms bandwidth and latency because i was more used to talking about them in terms of network latency and bandwidth, not in terms of a singular operation or program. So i did some research on the network latency and bandwidth and figured i would share what i found in a laymen's terms for those who might be mixed up like i was (the below notes are taken from various sources):
What is network latency? It describes the delays involved with Internet connectivity. A lower latency simply means a lower delay time, giving us the perception of faster network speed, although it might not actually be faster technically. A high-latency connection has more delays and performs more slowly. You can measure latency with ping tests to determine how many milliseconds it takes for a test data set to travel from one computer to another. Gamers know what i'm talking about
So why is it important? High-latency levels create data bottlenecks and unacceptable lag that hurts the performance of the entire network. High-latency networks in an office, for example, can hurt productivity and hinder your ability to respond in an environment that demands fast response times, such as the news media or the stock exchange (I think this example was brought up in lecture too). Gamers always try to modify their computers to chase lower latency and are constantly modifying their connections to reduce lag and enhance their performance in their favorite games.
What is bandwidth? Lets look at your internet connection as an actual pipeline. Then, bandwidth would be the width and breadth of your pipe. A larger pipe means you can send more data though. Therefore, more bandwidth means that you can pass a lot more data through your connection in the same amount of time. Most Internet service providers represent bandwidth with a measurement of megabytes per second.
Why is bandwidth important? The more bandwidth you have, the more information you can send through the Internet without realizing a slowdown or reduced performance. For example, if you're on a 30 Mbps connection, you can tax it with multiple downloads and traffic and realize excellent performance as long as you don't exceed a combined 30 Mbps limit.
This comment was marked helpful 0 times.
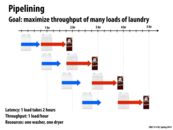

Why is the throughput 1 load/hour? Isn't it 4 loads in 5 hours, so .8 loads/hour?
This comment was marked helpful 0 times.

I think throughput here refers to a potential throughput given this pipelining scheme. If we carried this process out ad infinitum the overhead of the initial wash and the final folding would be negligable compared to the time spent drying so our throughput would approach 1 load/hour.
This comment was marked helpful 1 times.

Correct. The steady stage throughput is one load per hour.
This comment was marked helpful 0 times.


It might be interesting to note that one optimization to the classic RISC pipeline is to forward data from later stages to minimize stalls. In the classic pipeline here, it is not until the writeback stage that the decode stage can get the latest data from computation. So one way to decrease the stall that might happen is to forward data straight from the ALU in the execute stage, to the decode stage.
This comment was marked helpful 0 times.

Question: Let's say the "execute" phase of the above pipeline took significantly longer than the other pipeline stages. What might you consider to speed up the pipeline's execution?
This comment was marked helpful 0 times.

Maybe you could build some sort of specialized hardware that was optimized for the execute phase (if this was a frequently used enough construction that that was worth the money/effort), and then have a dedicated thread just running the execute phase while the others cycle through the other phases.
This comment was marked helpful 0 times.

We could speed up the pipeline's execution by having multiple ALUs. That way we could fetch and decode more instructions and write back more data while waiting for one execution to complete, ensuring that the other resources are always kept busy.
This comment was marked helpful 0 times.


The buffer here "slows down" the speed of input. As mentioned in class, the speed of the whole pipeline depends on the slowest stage, that is, the blue blocks in the picture. If there is no buffer, the high-speed input floods into the slowest stage. Obviously, the blue stage has its hands full and has to drop the coming jobs. Although the picture of non-buffered pipeline may look like the same (only the gaps between the orange and blue parts are gone), there are actually jobs dropped.
This comment was marked helpful 0 times.

In my opinion, Buffer is critical for pipeline in the following aspects: 1. From the slides, we could see the buffer always ensures the immediate input for the slowest stage(blue block), so we are able to keep the slowest stage busy to maximum efficiency. 2. I think it also eases programming. Say if you have no buffer, it would be tricky to coordinate different stages in the pipeline. You have to know when the blue block is available before getting results from orange block.
This comment was marked helpful 0 times.

I think another reason for buffering that hasn't mentioned that it allows for bursts of activity to be handled more efficiently. In the example above, we see that the processor can only send four messages consecutively before it has to wait for the blue block. If we are able to buffer messages, than the processor can send many more messages consecutively before waiting. So I think buffering will be beneficial when we expect a slow stream of requests interleaved with short bursts of high activity.
This comment was marked helpful 0 times.

So in a way the critical path determines the overall speedup for the whole pipeline.
This comment was marked helpful 0 times.


When the slide says, "what really matters ... cost of the computation fundamental to the problem", is it referring to the part of the communication that is causing the highest cost (i.e. the part with the slowest speed) and determining the overall cost of the communication? Why is that part fundamental to the problem otherwise? Also, so if I was to write out the communication cost in a Big-O type of format would it be T(n) = O(cost of slowest part) + (constant time of other work)
This comment was marked helpful 0 times.

I guess that's an okay way to represent the communication cost in big O, but I think what it means in the slide by "cost relative to the cost of the computation fundamental to the problem being solved" has to do with how the potential benefit from solving the problem in parallel. Basically, if the cost of communication is roughly equal to the cost of solving the problem in serial, there's no benefit to running in parallel. I think all it's saying is that 5 ms communication cost is great if the computation cost to solve the problem in serial is 5 minutes, but terrible if the computation cost is also 5 ms.
This comment was marked helpful 0 times.


If we assume that communication between the threads is costy, then one possible improvement for this scheme is instead of passing between the threads one row above and below, we pass two each. So for example P2 would work on row 2 through row 8 (one-indexed) and P3 would work on row 5 through row 11. With 2 overlapping rows between each block, every thread can now run two iterations before having to update the overlapping rows. However every update would need to send and receive twice as many rows as before, but this may still take roughly the same time because the data transferred is unlikely to exceed the bandwidth and latency is bottlenecking the performance
This comment was marked helpful 0 times.

I don't think I understand your solution, @pingshaz. If the row overlaps, then P2 still must communicate to P1 row 2's new status. If you are alternating which block these boundary rows belong to with every iteration, well, it doesn't help because you're still dependent on the rows below/above from the change of the previous iteration, I don't see how you can go two iterations and still correctly modify the boundary rows.
This comment was marked helpful 0 times.

Well, in general if we only want to compute the results of 3 rows after one iteration, we need the row above and below as our dependencies. If we need to know the results of them after two iters, we need two rows both above and below. So my idea was to do two iterations and communicate the four dependency rows in one go. I wasn't alternating the boundary assignments. For example, in my scheme, row 5 through row 8 (one indexed) belongs to both P2 and P3 all the time. So there is actually a fair bit of repeated computation. But in some cases it's worth the hassle because communication is expensive.
This comment was marked helpful 0 times.


In our blocking assignment, we must communicate the top and bottom row of each assignment which is where we get our 2PN term. There are 2*N communications per block, and P blocks/processors in this example. On the interleaved assignment, each row must be communicating twice since there is a dependency on the rows above and below it. Thus, the interleaved assignment has a total of ~2N^2 elements communicated, and a total of N^2 computed which gives us the ratio of 2.
This comment was marked helpful 0 times.


I'm still a little confused on this slide. Could someone please explain to me why the number of elements communicated per processor is $ \frac{N}{\sqrt{P}} $?
This comment was marked helpful 0 times.

The number of elements communicated per processor is exactly the perimeter of each block. Because these blocks are relatively square, and the area of each block, or the number of elements computed per block, is $\frac{N^2}{P}$, the side length of each block is $\frac{N}{\sqrt{P}}$. Thus, the perimeter of each block is $4\frac{N}{\sqrt{P}} \propto \frac{N}{\sqrt{P}}$.
Of course, these numbers are not entirely accurate since it is very unlikely that $\frac{N}{\sqrt{P}}$ will be a nice whole number, but they are still useful for comparing asymptotic complexity.
This comment was marked helpful 0 times.

You can also intuitively imagine that the communication cost is proportional to the perimeter of each region of work. A square thus minimizes the perimeter:area (ie. communication:work) ratio.
This comment was marked helpful 0 times.


Is this just called "arithmetic intensity" to refer to how much of our processing time is utilizing the ALU?
Because it seems like we could just say "computation-to-communication ratio" and it would be more clear.
This comment was marked helpful 0 times.


I'm not quite sure what exactly inherent communication is. If artifactual communication covers everything related to how communication actually occurs (on the system level, at least), then how does knowing how communication occurs in ideal circumstances help us understand how communication actually works? Or is my understanding of artifactual communication flawed as well?
This comment was marked helpful 0 times.

Inherent communication is what the program requires, typically in program and how you write the program, it is minimum communication needed. But artifactual communication happens in the hardware implementation, like the cache line example which the programmer do not expect, so it would be slower if something undesired happens in the hardware.
This comment was marked helpful 2 times.

I think one example of artifactual communication would be retransfer of lost packets in the TCP protocol. The program does not inherently require this retransmission, yet it is needed in practice due to imperfect communication channels. Another example would be the SYN packet when we start TCP, since if communication channel were perfect, we would not need the receiving node to send a SYN to the node who started the connection.
This comment was marked helpful 0 times.

@uhkiv
I believe the SYN packet constitutes inherent communication. I believe the line is drawn at the point where it becomes unnecessary to send the data in an idealized world. A node necessarily needs to know that another is communicating with it to initialize the actual transfer of data. Similarly the sending node needs to know that the communication is possible at all.
However, I believe your point brings up the fact that the abstraction level of this definition is not rigorously defined. Is the communication of the size of the data artifactual? I'd argue it isn't, because it could not possibly be known by the processor beforehand. But we are idealizing to have "perfect knowledge about what is needed to communicate," which makes this unclear.
This comment was marked helpful 0 times.

I'd argue that sending the size of the data is artifactual communication, since you don't strictly have to send a certain amount of size data to solve the problem. You could send less size data by sending more data per message (and therefore fewer messages).
This comment was marked helpful 0 times.

I don't know if I agree with that, ben. Simply because you could send it in a smaller size doesn't mean that it is better to do so. Perhaps each message is independent and it doesn't make sense to group them together, and you would like to know the individual size anyway (such as instant messaging). In general I disagree with the notion that because you can compress the data being sent, it is somehow better. For example, compressing a file might mean that you're sending "less" data but if the latency is low enough you would not want to tar and untar a file every time you send it across.
This comment was marked helpful 0 times.


Cold miss(compulsory miss): First reference to any block would always be miss, usually happens at the start of a program since data has not been accessed before, unless the block is prefetched. Could be reduced by increasing block size of prefetch.
Capacity miss: miss due to cache size is limited, could be reduced by building a larger cache. But cache size are always limited for fast access, so a hierarchical L1, L2, L3 cache structure is used.
Conflict miss: miss due to associativity, would have a hit with a fully associative cache. But fully associative cache is limited by the associative search for all the locations, so it is slow and not very practical.
Communication miss: miss due to transfer of data between different caches, would cause a big problem if data ping-pong between caches. For example, different processors need to update a location which is shared, in shared memory system, always need to get exclusive access state before write the data.
This comment was marked helpful 0 times.

Question: I understand that cold misses occur when data has not yet been accessed and therefore can't be in the cache already. This slide notes that they are "unavoidable in a sequential program". Are they therefore avoidable in non-sequential (I'm assuming this means parallel) programs?
This comment was marked helpful 0 times.

@moon: I don't think that cold misses are avoidable in a non-sequential program. The point of a cold miss is that it happens as a result of the cache being empty, which is true at the beginning of a parallel program as well. I think the only way to avoid a cold miss is to do some sort of pre-fetching data to populate the cache, but this would also result in a cold miss while prefetching, so it isn't really a solution.
This comment was marked helpful 0 times.

Consider a program with two threads running on a processor with two cores and shared cache between the cores. Thread 0 reads address X for the first time causing X to be loaded into the cache. Then, at some later point thread 1 reads X for the first time. While by definition this should be a cold miss for thread 1 (this thread has never accessed this data before), the access is actually serviced by the cache since it was previously loaded by thread 0. In a sense, thread 0 has effectively prefetched the value for thread 1, so from thread 1's perspective it avoided what otherwise would have been a cold miss when considering the behavior of thread 1 alone.
This comment was marked helpful 0 times.


I just want to confirm that this is true:
In increasing the cache size, so that it starts to cover more of the a working set but not all of it (so if you were moving between the drop off after the first working set to right before the drop off for the second working set), you can store more things in your cache, so the data traffic decreases because of fewer capacity misses. However, it does not decrease as much because since you are not covering the entire working set, there will be conflict misses that replace cache lines. Is this the reason why it does not increase as dramatically as it does after covering the entire working set?
This comment was marked helpful 0 times.

@ycp: yes, that's a very plausible description of behavior that could create this graph.
Another situation would be a case where the access pattern is streaming over an array over and over again:
while (!done) {
for (int i=0; i<N; i++) {
// do something with A[i]...
}
If the array is larger than the cache, all values of A will need to be fetched from memory (due to capacity misses). If A fits in cache there there are no misses. So in this case instead of trending down slightly the curve would be completely flat until the cache size could hold all of A, then it would drop sharply.
This comment was marked helpful 0 times.


The reason the above works is because since each element requires elements from the points around it, there would be more reuse of data (and thus better cache utilization) if we use blocks of data rather than just rows. If the cache can only hold one row, then in the first implementation the cache would have to be updated each time we try to access data from a row above or below an element.
This comment was marked helpful 0 times.


Of course, if several threads working on the same data structure are running at the same time, then there is a chance that a lot of them will be waiting for locks in that data structure if it has them. Even atomic operations on a GPU can have this problem--several threads atomically modifying shared data, even though they will have great locality, will potentially spend a lot of time waiting for exclusive access.
This comment was marked helpful 0 times.

That doesn't really detract from the importance of co-locating the tasks, however. There's two cases:
- The threads aren't trying to get a lock on the data structure. Then co-location provides all the benefits as noted in the slides above. Greater memory efficiency, less communication, etc.
- The threads need a lock on the data structure. In this case, it wouldn't matter how closely or far apart they're scheduled. The bottleneck is the lock and the scheduling of the threads doesn't affect that. If anything, you might see minor performance gains from the memory locality.
This comment was marked helpful 0 times.


When we read one element that is not in the cache, we will read a whole cache line. But does that really matter? Sequential read is very fast and most of the time is spent on the latency to initiate the read. This is the time we cannot avoid. So I really don't think read 64 bytes data will need much more time than reading 1 byte.
This comment was marked helpful 0 times.

I agree, though I don't think that's the point this slide is trying to make (I may be wrong).
The bigger issue is that if your memory layout is inconsistent with your access patterns, you'll have a lot of costly cache misses. I think the above picture is just illustrating what we learned in 213: if the array is stored in row major order, but we iterate through the array column by column, we won't be effectively using the cache.
This comment was marked helpful 0 times.


If two processors both tried accessing each other's cache lines, problems could occur.
P1 would ask for the cache line, load it from memory (slowly), and finally have access. Then, possibly before P1 could finish its work, P2 would ask for the cache line, invalidating P1's cache line, and making it move all the way through L3 cache to get over to the different processor.
This "ping pong" effect of the cache line would result in a lot of invalidation and waiting, rather than progress.
This comment was marked helpful 0 times.

I agree with @smklein's explanation, but whether making cache line move all the way through L3 cache depends on the design. If cache to cache transfer is provided, then the data could be directly transfer to the other cache line using whether bus based or directory based structure and protocol.
This comment was marked helpful 0 times.

This example from the wikipedia page helped me a lot in understanding how false sharing is a real thing:
In the code below, we observe that the fields in the instance of struct foo will be on the same cache line (assuming a cache line size of at least 8 bytes). We then launch two functions on two different processors, both using the same instance of struct foo. One method (sum_a) only reads from f.x. The other method (inc_b) writes to f.y the incremented value.
Every time the inc_b function increments f.y, the processor running the inc_b function sends out a message over the interconnect, informing the other processors that they should invalidate the cache line, due to modification. Unfortunately, those modifications are disjoint from the reads that the other processor (running sum_a) makes.
Therefore, it would be ideal that no invalidation should occur, but since the smallest level of granularity that the system works in is in terms of the size of a single cache line (artifactual communication), there will be a significant amount of 'thrashing' in this code.
Python:
struct foo {
int x;
int y;
};
static struct foo f;
/* The two following functions are running concurrently: */
int sum_a(void)
{
int s = 0;
int i;
for (i = 0; i < 1000000; ++i)
s += f.x;
return s;
}
void inc_b(void)
{
int i;
for (i = 0; i < 1000000; ++i)
++f.y;
}
One solution to this problem would be to add padding between the x and y fields, so that they are on different cache lines. For example, if the cache line was 8 bytes in size, we could use the following struct definition to avoid false sharing:
Python:
struct foo {
int x;
char c[4];
int y;
}
Now, the writes to f.y will not interfere with the reads from f.x. This struct definition is more cache-friendly, but of course, it incurs a substantial memory footprint.
This comment was marked helpful 1 times.

Thinking back to assignment 2, I guess one of the reasons why using a thread for each pixel was so slow is that the pixels in the image are laid out in row order, but if the thread blocks worked on squares in the image, there would be a lot of cache-ping-pong between the L1 cache for each SMXes on the GPU.
This comment was marked helpful 0 times.

I think one important thing that came up in lecture was that these artifactual communication isn't inherent in the code, but simply the result of hardware implementations. Thus it is hard to know exactly how these artifactual communications are affecting the performance of your program.
This comment was marked helpful 0 times.

@yanzhan2 In the intel x86 architecture, it is most likely that it passes across processors at the level 2 cache. This is because it needs to maintain inclusion throughout the cache hierarchy. Copying a value from processor 1's L1 to processor 2's L1 violates inclusion unless it updates processor 2's L2. This process of updating processor 2 L1 and L2 would be to large an overhead for an L1 cache, as it is intended to be extremely quick.
x86 seems to copy across from one processors L2 to another processors L2. This is suggested by the fact that reading from another processors L2 is faster than reading from L3 (slide 18).
This comment was marked helpful 0 times.

Is false sharing and artifactual communication the same thing?
This comment was marked helpful 0 times.

They're closely related -- false sharing is the pattern of accesses that causes the artifactual communication to occur
This comment was marked helpful 0 times.


Question: if we were already given the layout on the left, wouldn't we have to recreate the data in the layout on the right to minimize the artifactual communication? For operations involving 2D arrays, it doesn't seem likely that the data would be organized like the example on the right to begin with.
This comment was marked helpful 0 times.

Correct. This slide suggests that the data be reorganized in the manner shown at right in order to reduce artifactual communication during parallel computation.
This comment was marked helpful 0 times.

It is actually very common in performance critical applications to use this kind of array layout. There are generalizations to this 'block major' order such as Morton order. It makes some interesting reading.
This comment was marked helpful 0 times.

I'm kind of confused about what this 'memory layout' refers to. So is it the data structure we defined to feed our programs? According to this slide, we should define data blocks corresponding to work assignments of processors?
This comment was marked helpful 0 times.

Memory layout refers to how data in an application is mapped to the address space. For example, in a 2D C-style array, data is mapped to the addresses in row major order. A[i][j] is stored at address A + i*WIDTH + j; However the developer might choose to map elements of a 2D array to addresses in a difference way.
Challenge: Can someone write some code to compute the address of element A(i,j) where (i=row and j=column) in the "4D blocked layout", if the size of a block is BLOCK_X * BLOCK_Y elements and the dimension of the overall 2D grid is GRID_WIDTH and GRID_HEIGHT? For simplicity, assume BLOCK_X evenly divides GRID_WIDTH.
This comment was marked helpful 0 times.

I'd like to check if this is correct:
int i1 = i/BLOCK_Y;
int j1 = j/BLOCK_X;
int block_no = i1 * (GRID_WIDTH/BLOCK_X) + j1;
// Address of start of block
int block_start = block_no * BLOCK_X * BLOCK_Y;
int i2 = i % BLOCK_Y;
int j2 = j % BLOCK_X;
return block_start + i2 * BLOCK_X + j2;
This comment was marked helpful 0 times.

An extreme example where blocked 4D array layout helps is when the working set doesn't fit in physical ram and some parts of it are paged out - if there were only a few threads working on many blocks, the row-major array layout would cause lots of pages to be paged into DRAM for each block, whereas the blocked array layout would only cause one or two pages to be paged in.
This comment was marked helpful 0 times.

@eatnow, don't you have X and Y mixed up in your code? I think that you're finding A(j,i) instead.
This comment was marked helpful 0 times.


We had an example in class that involved three people walking across the room to shake Kayvon's hand. To abbreviate, I will refer to the three people as "A, B, and C", and Kayvon as "K".
Initially, A, B, and C walked across the room at the same time, and then waited, in order, for the previous person to be done shaking K's hand. This made the latency for B's request higher, which made the latency for C's request higher.
The example showed the "contention" part of this slide, and how to reduce it -- the suggested solution involved staggering the requests, so B and C did not have to wait to shake K's hand.
This comment was marked helpful 0 times.

Wouldn't staggering the request still eventually result in the same total time? What I had in mind is suppose shaking hand takes 1 second and travel time is 4 seconds.
We stagger the request as follows:
A,B,C are all ready at t=0
- A leaves at t=0
- B leaves at t=1
- C leaves at t=2
- A arrives at t=4 then leaves at t=5
- B arrives at t=5 then leaves at t=6
- C arrives at t=6 then leaves at t=7
- A returns at t=9.
- B returns at t=10.
- C returns at t=11.
And this is what happens if we schedule them in bulk:
A,B,C leaves at t=0
A,B,C arrives at t=4
- A leaves at t=5
- B leaves at t=6
- C leaves at t=7
- A return at t=9.
- B return at t=10.
- C return at t=11.
As I see here A still takes 9, B takes 10, and C takes 11. Also if we schedule things in bulk can't we then use some technologies that deal with bulk data, e.g. in the case of network io TCP delayed ACK or bigger MTU size (Jumbo frames), to reduce total communication?
Edit: formatting
This comment was marked helpful 0 times.

I believe that the advantage of staggering the handshakes goes back to the whole pipelining of tasks concept. If our program's goal is to simply create three handshake requests and send them for approval, it might not make sense to stagger the handshakes if all we care about is time.
For example, say we have a program that has to construct a request, send the request to a web server, and then once the request is processed by the server start to pull data from the server. In this example, constructing a request might take some time. If synchronize the requests into a block before sending it to the server, we are minimizing the concurrency of the requests and therefore increasing the communication cost (as per the formula given on a previous slide). In this example, the t_initial for the blocked request would not be t = 0, but rather t = max (time to make request)
This comment was marked helpful 0 times.


For anyone interested, you can catch the demo here, starting at 1:09:25 (it's about 4 minutes long).
There's some good discussion on the previous slide, but here are some of the highlights:
- 3 students needed to talk to the processor (Kayvon); initially at the same time.
- The burst caused contention because it took some time for Kayvon to shake each hand.
- Next the students walked to Kayvon in random order.
- Pipelining these "requests" reduced contention.
This comment was marked helpful 0 times.
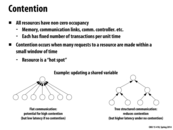

In lecture, after the contention demo it was asked how we might solve the problem of multiple requests contending for the same resource, specifically without changing our set of resources. The accepted suggestion was to stagger our requests--let R1 get sent out, wait a bit, then send R2, and so on.
This doesn't really solve anything, though, right? Holistically speaking, we're still spending just as much time as if all the requests waited for the resource simultaneously. Staggering gives each individual request the illusion that it got instant access to the resource, but no time was saved overall.
What kind of use cases exist for this kind of solution which solves the problem on a request level but doesn't reduce our overall time spent?
This comment was marked helpful 0 times.

Maybe if there was some other work that each person needed to do, then the second person could start on that work during the staggering time (like if each person both needs to walk to Kayvon, shake hands, and come back AND read a few pages of some book, then person A could start walking while person B reads at first and then later starts walking - this would make the total time spent for both people to complete their operations less, much like the laundry example).
I definitely agree that it won't give any benefit in this specific case though, if there's nothing for the people to do while waiting to be sent to Kayvon.
This comment was marked helpful 0 times.

Also, the students in our in-class demo were very well-behaved and waited their turns without having to settle who got to shake hands when. There are some lock implementations for which the work of arranging who gets access to the resource in what order is non-constant with respect to the number of waiting people, and can in fact get quite large. In such a situation, the sum latency across all the requests would be worse if they arrived at once than if each arrived just as the previous one was done. My understanding is that this sort of thing will become particularly important once we start talking about cache coherence.
This comment was marked helpful 0 times.

Possible situation 2: the number of requests coming in is very very very high (say you're Google, for example, and updating some sort of global info every time a query comes in). Now, suppose our locking scheme is perfect so the problem I posed above isn't an issue; you might still encounter slowdowns because storing a large number of requests waiting on a lock takes space, and could easily grow your working set until it overflows your cache. If that's allowed to happen, then either your server must be overprovisioned so that it can still handle requests fast enough (which is expensive), or users could start to experience high latency spikes. Making the stream of requests more regular by stalling some of them would make the behavior of the server more predictable.
This comment was marked helpful 0 times.

Related to this github from piazza: https://github.com/awreece/codearcana/blob/master/content/performance/achieving_maximum_memory_bandwidth.md
The author ends the post with some of the following unanswered questions:
- Why doesn't the use of non-temporal instructions double bandwidth for the single core programs? It only went up 50%.
- Why aren't the AVX instructions on one core able to saturate the bandwidth ?
These problems are focusing on why full memory bandwidth was not achieved using a single core, even using SIMD execution and non-temporal instructions (doesnt save to cache). Could the reason for this underutilization be because of contention? When the same code is run on multiple cores, suddenly the theoretical max bandwidth was achieved. Contention here makes sense since a single core would not be able to handle that much memory at once (or rather would be slowed by contention), while multiple cores would not face this problem (or face this problem to a lesser extent).
This comment was marked helpful 0 times.

I'm not sure I understand. Contention is between threads, so if the code is being run on only one core, then I don't see how there can be any contention at all. Would you mind going into more detail?
This comment was marked helpful 0 times.

Pseudocode for implementing barriers using messages:
I imagine we would delegate one thread as master, who will run the following:
for (int i = 0; i < num_procs - 1; i++) {
sync_recv(chan0);
}
// now master thread has received notification from every thread
for (int i = 0; i < num_procs - 1; i++) {
async_send(chan1);
}
And the other threads will run the following:
async_send(chan0); // notify master thread
sync_recv(chan1); // wait for master to notify back
This corresponds to the flat communication on this slide. The "hot spot" in this case is the master thread. If the number of threads is too high, this simple implementation might be too slow. I think a way to solve it is to have a way to broadcast a message to a group of threads, instead of sending one message at a time.
This comment was marked helpful 0 times.


Question: is R/W counted as a conflict, or they are using different wires?
This comment was marked helpful 0 times.

Unless I'm missing something, all 32 threads do the same thing on each clock cycle, so that situation (some threads reading and some writing) can't arise.
This comment was marked helpful 0 times.

Wait, that wasn't quite right. If this memory is shared across the chip then all currently running warps could access it. However, I don't think they can access it during the same clock tick since we only have 1 batch of 32 load/store units that all the warps have to share. I could be wrong again though.
This comment was marked helpful 0 times.

@mchoquet. This is a GTX 480 specific example. You're referring to the GTX 680. For the sake of understanding this particular example of contention, consider a single banked on-chip memory (as illustrated above) and a single 32-wide warp trying to access it.
Shared memory address x is serviced by x mod 32. And each bank can service one request per cycle, unless all requests are to the exact same address (special case 1).
The overall point is that this is an example of contention playing a big role in the actual cost of an operation. 32 loads with no contention are completed in one cycle. If contention is present, the 32 loads could take much longer.
This comment was marked helpful 0 times.

I really like this example. There are too many situations so that NVIDIA can't handle them all. They decide to have the special case that if all threads access the same bank, and discard the situation that all threads access two banks. Maybe bulk load's overhead is too high. And [3*index] doesn't have the problem because 3 is not a factor of 32, we are just lucky.
This comment was marked helpful 0 times.


Out of all of the solutions, I feel that this one seems to have the most dependency on the amount of data. By this I mean that both the extra memory used for computation and sorting as well as the computation time depend on the amount of data. In this scenario, having more particles increases the array size, and also increases the time required to sort the array. Another solution presented which used finer granularity locks, could require the same amount of computation time for small and large data sets if the particles don't conflict.
This comment was marked helpful 0 times.

So one thing to take away from this lecture is to make sure to correctly organize data for the processors so that our cache misses are lowered?
This comment was marked helpful 0 times.

I would rephrase that as data that is well organized can reduce your cache misses, which is useful only if the program itself exhibits good locality. If the process of re-ordering / reorganizing the data is very time consuming in comparison to the actual computation that occurs afterwards, it may not be worth it.
This comment was marked helpful 0 times.

To add a bit to what @RICEric22 said, another thing to keep in mind is load balancing. Locality is good, but remember the Mandelbrot example from homework 1. In that case, we actually made it significantly faster by assigning threads data that are further apart than assigning by contiguous blocks. While this potentially hurt locality, load balancing was greatly improved.
Overall, locality is something to keep in mind, but there are many factors that should be weighed in when thinking about distributing data.
This comment was marked helpful 0 times.

















It actually took me until this lecture to realize that the quotes about how X song really relates to parallel computing weren't actually real...
This comment was marked helpful 0 times.
What are you talking about? They're all real.
This comment was marked helpful 3 times.