

I got lost at this slide. Why neither of the two loops are parallelized by ISPC?
The outer for-loop is run in parallel, right?
This comment was marked helpful 0 times.

@yetianx: A solid question. Anyone?
This comment was marked helpful 0 times.

When we call the sinx function, a gang of n program instances is created (where n is equal to the SIMD width of the processor). Each program instance executes the sinx function on disjoint sets of array elements. So, the program instances run in parallel on the processor.
However, the execution of a single program instance is entirely sequential. The program instance obtains its data set to work with via the outer for loop, via a set of indices into the input array. The inner for loop is simply used to compute the sin of a specific array element.
So, if the SIMD width of the processor was 4 and we had a set of 12 array elements, then the work would be divided among the program instances in the following manner (in terms of indices of array elements):
- Program Instance 0: 0, 4, 8
- Program Instance 1: 1, 5, 9
- Program Instance 2: 2, 6, 10
- Program Instance 3: 3, 7, 11
Note that using the foreach loop instead of a for loop would not change this fact. The ISPC compiler may choose a different way of assigning work to the program instances; the foreach construct just serves as a hint to the ISPC compiler that it is safe to launch multiple program instances to execute operations on the data set. By doing so, the programmer is no longer responsible for assigning work to the program instances.
Edit: foreach just points out that the iterations of the loop can be executed using any instance in the gang in any order, as clarified by @kavyonf below. So, the ISPC compiler could potentially choose a completely different program instance assignment than the one shown in the program on the left, such as this:
- Program Instance 0: 0, 1, 2,
- Program Instance 1: 3, 4, 5
- Program Instance 2: 6, 7, 8
- Program Instance 3: 9, 10, 11
Such an assignment would not be optimal from a spatial locality perspective (see here, but it is a perfectly legal assignment policy for the ISPC compiler to adopt, as each program instance works on a different set of data elements.
This comment was marked helpful 6 times.

@arjunh: Perfect (and super clear). Except... the statement "the foreach construct just serves as a hint to the ISPC compiler that it is safe to launch multiple program instances to execute operations on the data set".
No launching is going on at the start of the foreach loop. The instances have already been launched, as you state, at point of call to sinx.
The foreach construct declares that it is acceptable to execute iterations of the loop using any instance in the gang and in any order.
This comment was marked helpful 4 times.
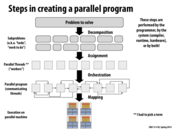

I mentioned in class, and I want to mention again, that this diagram was meant to assist discussion of general process of creating a performance parallel program. I urge you to not rack your brain trying to establish a precise definition of terms like decomposition, assignment, orchestration, and mapping. There is no one set sequence of steps for creating a parallel program, and decisions made in one phase of this diagram are highly related to decisions in other phases. For example, you might choose a particular assignment because it makes orchestration easier or decreases overheads of communication.
This comment was marked helpful 0 times.

Decomposition- how do you divide you workload, down to what granularity do you decompose the workload. One might choose a method of decomposition while taking into account assignment, mapping, orchestration and maybe mapping.
Assignment- In the case on the slide above we see the work being distributed among parallel threads but depending on the API or Abstraction/Programming model you are working with what work is assignment to what programming construct will vary.
Orchestration- How is Synchronization and communication done in order to ensure program correctness.
Mapping- Typically done by the device being programmed, mapping is somewhat predictable as it corresponds to the Programming semantics available.
This comment was marked helpful 0 times.


What, precisely, does it mean for a fraction of the execution to be inherently sequential? Suppose there is a program that has a more complex dependency structure (e.g. not a binary tree or a linear pattern), where different steps of the execution have different numbers of dependencies. How is S computed?
This comment was marked helpful 0 times.

I think it means that part of the program must run sequentially, and could not possibly be parallelized. For example, maybe each loop iteration depends on the result of the previous iteration. S would be computed in terms of the percentage of work that must be performed serially. For example, in the practice exam question 1, the first for loop was parallelized and the second was not, so S was 0.5, and the maximum speedup was 2x. However, if the first loop was more work intensive, S would be less because less work would be done in the second loop. However, I'm not sure about more complex dependency structures, and I am also curious about how to calculate S in those scenarios.
This comment was marked helpful 0 times.

If different steps of the execution have different number of dependencies, wouldn't S simply be the longest path of dependencies? I'm not sure I understand what makes this so complicated.
This comment was marked helpful 0 times.

It's just the equivalent of the "span" of the program from 150/210. Although in the real world, our speed-up will be a lot less than 1/s because it's difficult to perfectly parallelize the parts of your program that are dependent.
This comment was marked helpful 0 times.
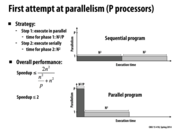

For anyone confused about the speedup equation, here is a quick summary.
The original execution time was 2 * n ^ 2.
The new execution time is (n ^ 2) / p + n ^ 2, as the first half has been split over p processors.
To make the equation seem more intuitive, observe behavior as p approaches either 1 or infinity. If p = 1, there is no parallelism. The speedup simplifies to be 1x. If p = infinity, then the speedup simplifies to 2x. This is because half of our program is still sequential.
This comment was marked helpful 2 times.


So here we discussed interesting tradeoffs between keeping the final addition of sums as a linear operation rather than implementing a reduce or something similar to parallelize the final addition. What we found that if P >= N, the + P addition term starts to play a significant role in the total computation time of the problem.
Overall, if we are working on a high pixel density image with a standard multi-core computer, the extra synchronization management needed to distribute the reduce might start to outweigh the benefits of changing the +P term into a +log(P) term.
However, if we are working on a supercomputer with a bajillion processors to process a small image, we find that there will be processor idle time or large waste of time trying to optimize the final addition
This comment was marked helpful 0 times.

Here wouldn't it be possible now, with the phase 2 change, to merge phase 1 with phase 2? As now we can just combine the step of increasing the brightness with the computation of the partial sum on each pixel.
This comment was marked helpful 0 times.

@sss: I like your thinking. Could you elaborate more on your proposal to "merge"? Why do you think would that idea might improve the performance of the program as compared to the two-step strategy discussed above?
This comment was marked helpful 0 times.

Here I feel that having a phase distinction means that: Only when all processing in phase 1 completes then the computation of partial sums begins. Which I think would be fine the case of small images where every pixel can be computed in parallel, and all pixels are done in 1 computation step; however in the case of large images, once the computation on that pixel group is done, the threads might as well perform some phase 2 computation, as it's already loaded, for the group and write a final value into memory. This is so that that group of pixels doesn't have to be touched or cared about again. I think this'll save some IO memory loading as well as context switching.
This comment was marked helpful 0 times.

good! But let me try and explain in the terminology of the course.
By reordering the computation, you are able to reduce its bandwidth requirements by performing two operations each each time you load a pixel rather than just one. Note that you have not changed the amount of computation done. So your transformation has increased the arithmetic intensity of the program (or, in other words, reduced the communication-to-computation ratio).
The program was changed from:
// step 1
for (int i=0; i<N; i++)
pixel[i] = increase_brightness(pixel[i]);
// step 2
float sum = 0.f;
for (int i=0; i<N; i++)
sum += pixel[i];
float average = sum / N;
To:
float sum = 0.f;
for (int i=0; i<N; i++) {
pixel[i] = increase_brightness(pixel[i]);
sum += pixel[i];
}
float average = sum / N;
Notice that if N is sufficiently large that the entire image cannot fit in cache, then due to capacity misses the image will need to be loaded again from memory in the second for loop. The restructured code avoids this miss by performing both the brightness increase and the summation back-to-back, thus requiring only one load.
My code example is not parallel for simplicity, but this transformation works equally well in the parallel case as well.
This comment was marked helpful 2 times.


In class Kayvon said that Amdahl's Law is more like Newton's laws of motion and some people don't think it's any law at all. I was wondering why that was. I can see that it obviously doesn't take synchronization or communication overhead between the threads into account, so is that why? I'm sure there are other reasons as well.
This comment was marked helpful 0 times.

@jmnash: Sorry to disappoint, but it was a joke. I commented that "Amdahl's Law" despite its name, is more a simple fact than a deep fundamental truth about the world or computation in general. Physicists and theorists would certainly say that's a prerequisite for something to be called a "law". Systems folks have a considerably lower bar :-) ... leading to observations like Amdahl's Law and Moore's Law being handed names that ironically echo the great principles of the world.
This comment was marked helpful 1 times.


The data-dependency is unknown to compiler when using imperative programming language. Pure functional language with referential transparency makes it easier for parallelization during compiling time. I'm wondering whether you can always obtain similar performances with both imperative programming and functional programming. For instance, for problems, like the program 2 in assignment 2, whether it's possible to get a good answer without functional programming.
This comment was marked helpful 0 times.

Of course it is. Imperative and functional programming, as paradigms, are equivalent in most meaningful ways. For example, my program achieved good performance on program 2 and was a series instructions of the form "do this thing in parallel on this array, and as a result have program instances write to this other array". I could have written that as a series of map, scan, and some other higher-order functions, and then it could be considered functional programming, but I wrote it as a series of steps with side-effects and so I would argue that it was more in the spirit of imperative programming.
It's nice to think of parallelism in terms of higher-order parallelized functions, which lends itself to functional programming -- especially since we've all taken 210 which approached it in exactly that way. But I see no reason why actually implementing those functions requires functional programming.
This comment was marked helpful 0 times.


Something related we talked a lot about in Distributed Systems is task migration - we try to statically assign work so that it is balanced, but it can be hard to know how long each task will take. In certain cases, it might be best to re-assign tasks after initial assignment, in which case we migrate the task to another worker. Doing this is expensive, but could be faster or even necessary (if a worker dies, for example).
This comment was marked helpful 0 times.

Yes, except that I would point out that if a worker dies you cannot migrate the process but would rather have to restart the process on another node. I believe that "migrating" implies some way of transferring the work already done. If it is writing to a distributed file system, in theory you could try to find where it left off but I am not sure that it would be possible to tell that no data was corrupted.
This comment was marked helpful 0 times.


We can see here that the outer loop in the first program expresses how work is going to be split up for different program instances. In the second program the foreach statement offers a level of abstraction between the programmer, and the division of work. The foreach statement expresses the fact that there are no dependencies between any of the loop iterations, and therefore ISPC may set them up to be run in parallel.
I am curious about how ISPC would handle nested foreach loops.
This comment was marked helpful 2 times.
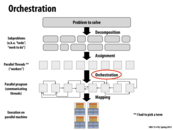

Assignment is often viewed from a math/algorithms perspective.
A program is modeled as a Directed Acyclic Graph (DAG), where vertices represent computation and edges represent dependencies (i.e. if computation X relies on computation Y, there will be edge Y -> X). Vertices are usually weighted based on relative computation time, and edges are usually weighted based on communication time.
The goal is then to assign tasks to the processors such that makespan is minimized, while making sure to respect all of the dependencies. This is NP-Hard, however, so most research focuses on developing heuristics.
More recent models also consider Mapping in addition to Assignment. The parallel computer can also be viewed as a graph, where the vertices represent processors and the edges represent communication links. Weights can be added in case the processors are not all equal. Mapping algorithms need to ensure that highly dependent tasks are placed in close proximity to keep communication costs at a minimum.
Finally, even more advanced algorithms are "contention aware", and avoid overloading any individual communication link in the network.
This comment was marked helpful 0 times.


Is there anything specific that must always be done during this step? The decomposition step mainly involves breaking the problem in parallel and sequential parts. The assignment portion is just that, assigning tasks to threads efficiently. Both those steps have a specific task that must be done. In that case, is the main general goal of the orchestration step making sure that threads are running smoothly and concurrently, and also trying to optimize in terms of memory and arithmetic intensity? It seems like there are many different routes to take in this step.
This comment was marked helpful 0 times.


I'm not sure what the last bullet point means about placing unrelated threads on the same processor to use the machine efficiently? When it says compute limited and bandwidth limited, does it mean to place these threads together such that they divide up the computational and bandwidth resources in the most efficient manner so as to maximize the use of these resources? If that is the case, would that not happen when the threads were on the same processor and had maximal locality/minimized communication cost? Can someone come up with a scenario where this is not the case?
This comment was marked helpful 0 times.

I think it's suggesting that the benefit from fully utilizing the resources of a processor might outweigh the benefits of locality.
For instance, if you had 4 "threads" and two processors to run them on, and 2 of those threads ran a program that was full of memory accesses, and 2 of those threads ran a program that had a lot of computation, it would make sense to assign 1 of each of those threads to a given processor; if you put both threads of the same type on one processor, that process could end up bandwidth-limited or computationally limited. Even if the threads of the same type have some locality, the benefit from being able to split the latency of the memory accesses could be worth it.
This comment was marked helpful 1 times.


Question from a student last year: What's an example of a problem where the mapping between work and data isn't very clear? Just wanted to hear about some cool examples.
This comment was marked helpful 0 times.

Mandelbrot set and the Square root program in the assignment.
This comment was marked helpful 0 times.

I think a particularly interesting (or annoying) example of a mapping and/or assignment problem would be problems where performing some unit of work could in turn spawn additional work, and the amount of additional work is not known until the work is performed.
A trivial example of this we saw in the very first lecture. We can try to divide summing up numbers among people, but if they are not given a balanced amount of work, then somebody is going to be idle while others are busy. They could have divided the work up evenly at the beginning, which people can do, but if we were asking a computer to divide the work up evenly this would be a sequential process limiting speedup.
A more complex example that I've had to deal with was trying to write a raytracer in CUDA. It's easy to divide the work up by mapping pixels to CUDA cores, but if a certain pixel needs to also send out a bounce/reflection ray, or a shadow ray, then now there is an imbalanced amount of work left to do as some pixels might not need further raytracing. Unfortunately without high end GPUs (at the time), CUDA did not allow for spawning additional work without communicating again with the CPU, which would have made the process so serial (and slow due to the PCIe bus) that it defeated the point of even parallelizing to begin with.
This comment was marked helpful 1 times.


Looking at the box-ed segment, it seems like each A[i,j] is dependent on all 4 cells around it : A[i, j-1], A[i-1, j], A[i, j+1], A[i+1, j]. So how is it that we claimed that each cell is dependent only on the ones above it and before it?
Edit: My bad, my question is answered in the comments of the next slide.
This comment was marked helpful 0 times.


Why is it that these dependencies only go right and down, and not also up and left when the code in the previous slide clearly uses all 4 adjacent array elements to compute?
This comment was marked helpful 0 times.

The code on the previous slide is using the array elements right and down as well, but only the array elements up and left have been updated so far (since the double loop is running row by row from top to bottom, and left to right within each row).
This comment was marked helpful 0 times.

I just wanted to solidify what benchoi said. When you're identifying dependencies in the above situation, it looks like what you want to do is to take a point and think about what computation needs to have been finished before the value at the point can be computed. From the code on the previous slide, which gives the sequential version, we know that the algorithm iterates through the array row by row from top to bottom, and from left to right within each row. Thus any version of the algorithm we design (i.e. a parallel one) can only match the sequential version if computation on a point waits for the element to the left and and the element above to finish first (and, relatedly, that it also occurs before the elements to the right and below).
I think it was also mentioned in class that this method is used to solve heat transfer or fluid mechanics problems. I might be wrong about this, but either way I think it provides a nice visual (and maybe a little too poetic) way of thinking about dependencies, if you imagine some source at the top left that spreads a material through the array, and the material can only reach a point if it has already reached the points to above and to the left.
This comment was marked helpful 0 times.


The key insight that makes parallelization possible here is that work for each cell only depends on the cells immediately to the left and above. Thus, by doing work in diagonals from the bottom left to the upper right, anytime we do work on a cell, we know that the cells above and to the left of it have already been updated in previous diagonals. Additionally, since within each diagonal, no cell is directly above or directly to the left of any other cell, we can update each of those cells in parallel.
This comment was marked helpful 1 times.

If the processing of pixels took variable (and large) time, a better algorithm would be to spawn a thread of execution for each pixel and each pixel would wait on its two dependencies before executing (using mutexes?). This way we make sure that every no core has to sit idle while a diagonal is finished.
This comment was marked helpful 0 times.

@achugh: let's say this grid was of modest size, say a mere 1000x1000. What might the problem be with creating one million threads?
This comment was marked helpful 0 times.

Maybe not all at the same time. You could use some smart look ahead scheme. Like say, when a pixel is getting processed- its grandchildren in the dependency graph get spawned. You would also need to avoid duplicate threads for a pixel. If performance is really important you may be ready to deal with the complexity. And on first look, this doesn't seem totally intractable.
This comment was marked helpful 0 times.

A guy mentioned a cool idea that we can use different threads to calculate different iterations. Another guy said we cannot make sure the second iteration runs slower than the first iteration.
Maybe we can do this with some synchronization.
Suppose we have 2 threads, 2 semaphore: sem1 init to 0, sem2 init to n/2(n is the num of rows).
Thread 1
while(some condition){
foreach row {
P(&sem2;)
starts to process two rows
V(&sem1;)
}
}
Thread 2
while(some condition){
foreach row {
P(&sem1;)
starts to process two rows
V(&sem2;)
}
}
Is that a possible solution?
@achugh: sem2 is needed when thread 1 finishes the whole matrix and begin the next iteration, when it has to wait until thread 2 goes ahead of it. Otherwise, if one thread only handle one iteration, we have to use as many threads as the total iteration times.
I did not notice there should be 2 rows between two iterations. So now two rows are processed between P and V. But I'm not confident about its correctness. Could someone give me ideas on this?
This comment was marked helpful 0 times.

I didn't completely understand the code, can you explain why is sem2 needed? Does it ever cause a wait?
Also, a cell the new Gauss-Seidel iteration would depend on the on the old iteration's cell on the right and the cell below it. So the old iteration needs to be 2 rows ahead of the new one.
This comment was marked helpful 0 times.


Couldn't this be a dangerous approach? If the error threshold changes because you're using a different metric or something (I don't know too much about the domain area), then your code is now completely broken.
This comment was marked helpful 0 times.

We set the error threshold before we start the iterations. The point here is that different algorithm might give us slightly "different solution", but as long as the solution converges to within error threshold, the algorithm is still valid.
This comment was marked helpful 0 times.
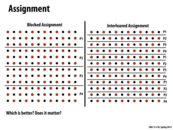

It seems to me that the blocked assignment is preferable because of locality, and an interleaved assignment would be more appropriate for situations when the the blocking assignment would lead to poor distribution of work.
This comment was marked helpful 0 times.

@benchoi: and for the solver application example used in this lecture, are you particularly concerned about poor distribution of work in the case where the grid is equally partitioned?
This comment was marked helpful 0 times.

In this particular application, the Blocked Assignment is better, as we have a balanced work distribution (same amount of work per pixel). Even more, there's less data that needs to be communicated between processors (at most two rows need to be send), as we can see in Slide 29
This comment was marked helpful 0 times.

@benchoi The work performed per pixel is rather straightforward and static: take the average of itself and 4 neighboring pixels. Because of this, the blocked assignment would not result in a poor distribution of work like it would with some other problems (cough).
This comment was marked helpful 0 times.

I guess I'd like to clarify what kind of parallelism we're talking about here - multi threading on different processors? If so, then yes block assignment will be better since we will not have as much cache coherence issues and we will take advantage of spatial locality. However, if we are using something like ISPC where each program instance writes to a specific cell, then the data being read is stored in a shared cache in that core (assuming it fits) and we will probably want interleaved assignment.
Can someone verify/comment on this? I'm not a 100% sure if I'm thinking about this in the right way.
This comment was marked helpful 0 times.

@rokhinip If by Cache Coherence you just mean that there will be fewer cache misses then I think you are thinking right. I don't think there is any Coherence involved here. Everything else is fine.
This comment was marked helpful 0 times.

aside from cache issues, blocked in this case is better because it requires less communication. Realize that you have to communicate for every element that lies on the "border", and in the case of the interleaved every element lies on two borders of a partition.
This comment was marked helpful 0 times.


How expensive is it to broadcast/receive an update, especially as the number of processors goes up?
This comment was marked helpful 0 times.


Even on a single machine with multiple processors, I think that communication should happen here because the act of P1 writing into the row that P2 needs will dirty those cache entries, so that at some point in time, P2 will have to go to main memory or P1's cache to get the new data, instead of being able to use its own cache.
This comment was marked helpful 1 times.

I think P1 and P2 may not necessarily to be on the different cores, like hyper-threading. Then they just need to fetch the data from L3 shared-cache. Or, if they are just in different ALUs, then they can exchange data even faster.
This comment was marked helpful 0 times.

@black: you are completely right. However, in the context of this slide I was referring to the case where P0 corresponds to work done by processor 0, and P1 corresponds to processor 1. (I referred to processors when explaining the slide, but you can replace processor with core without any change to the argument.)
@Q_Q. Good comment as well.
This comment was marked helpful 0 times.


Are we able to abstract away the NUM_PROCESSORS part from allocate in the same way for_all and foreach does?
This comment was marked helpful 0 times.

@idl: I guess you could do so; the idea behind the function call allocate(n+2, n+2, BLOCK_Y, NUM_PROCESSORS) is to specify an assignment strategy regarding how the array elements are assigned to the processors. The strategy suggested as the better option in lecture was a blocked assignment, as it involved less communication among processors (fewer rows have to be sent to the other processors, as each processor already has all the data it needs to perform the algorithm).
This is quite similar to the notion of explicitly using a for loop, with programCount and programIndex, to specify which pieces of work the program instances should perform. We could also abstract away from stating those details and instead use a foreach construct to let the ISPC compiler figure out how to assign the program instances. I'm not sure, but the compiler program should theoretically be able to figure out how to assign the array blocks to the processors as well.
This comment was marked helpful 2 times.


The problem here is that we are locking i * j * k times per thread, where 'i' is the number of rows a thread has to process, 'j' is the number of red cells in each row, and 'k' is the number of iterations it takes to converge
A better approach (details on slide 35), is to compute a partial difference within the nested for loops, and after that add it to the shared 'diff' variable. Hence locking only once 'k' times, according to the previous notation
This comment was marked helpful 0 times.

I had a small question regarding the use of barriers, may be I am confusing CUDA threads with task, but from our assignment 1 all the tasks ran the same instructions, and when you didn't want the instructions to affect you you just mask out your lane. Since, CUDA also follows SIMD, my question was won't all the CUDA threads exit the for loop at the same time if they were all running the same instructions and hence removing the need of the 2nd barrier ?
This comment was marked helpful 0 times.

Who can answer Pradeep's question? (I like Pradeep's question.) Anotehr way to think about this question is: Do all CUDA threads in a thread block execute in SIMD lockstep?
This comment was marked helpful 0 times.

Yeah, I think I get it now. So just to lay down what I am thinking. For ex: suppose we have 256 CUDA threads/block we would need 8 warps to run them. Also in the NVIDIA chip described in class only 4 warps (128 threads) ran at any time, hence these 128 running in the first 4 warps would need to wait for the other 128 to actually run after them and finish executing. Is this the reason barriers are used ?
This comment was marked helpful 0 times.

@pradeep
I think you're right (unless your saying the first 128 threads run first and then the next 128 threads run). Think of an example like:
If processor decided to schedule the threads such that the first 128 ran to completion first and then the next 128 threads were run, then if there was a barrier there would be a deadlock. This is because the second set of threads would never make it to the barrier.
The processor is basically free to schedule the threads in any way it wants, but for the reason seen in the example, its generally interleaves them in some fashion.
This comment was marked helpful 0 times.


As we saw in threaded applications that we coded in 213, the need for locks results from possible race conditions on the values of variables. In this case, the race condition is on the value of diff. Note that locks are not especially beneficial to the efficiency of parallel programs because they serialize the execution around them, creating a possible bottleneck while one thread executes the code in the lock and others simply spin while waiting for the lock to free up.
This comment was marked helpful 0 times.

It's a good thing that while cores aren't getting faster, we're still getting more space. The more different cores/threads can work in their own space and save combining for the very end, the less negative impact locks will have on performance.
And now a joke:
"Knock-knock," "Who's th--," "Race condition!"
This comment was marked helpful 1 times.


There are various abstractions and implementations of locks(or atomic operation). Software semantics are needed for program correctness, and hardware implementation could be efficient.
As mentioned in later slides, locks could be implemented as spin locks or deschedule, and there are trade offs for these two types of implementation. Even only for spin locks, there are various implementation, each with different thought for performance, such as MCS lock, tick lock.
Also, hardware primitives are needed for the lock implementation, like compare and swap, which would guarantee atomic operations.
Besides, optimistic implementation transactional memory would fit the atomic{} semantics, which would eliminate unnecessary wait.
This comment was marked helpful 0 times.


Although the number of barriers can be changed, here is their rationalization for this program:
Barrier 1: Needed, otherwise a thread could add to diff in the line
diff += myDiff, and a different thread could reset the global diff to zero in the line
float myDiff = diff = 0.f immediately afterwards.
Barrier 2: Needed, otherwise a thread may determine that it is done with an unnaturally low diff which doesn't have the contributions from other threads.
Barrier 3: Needed -- other threads must compute if 'done' is "true" or "false" based on the line if (diff / (n * n) < TOLERANCE) before anyone has the chance to set the global diff back to zero at the beginning of the while loop.
This comment was marked helpful 5 times.

I believe the code can be slightly rewritten so that only the first two barriers are needed. The code after the for loop should look like:
lock(myLock);
diff += myDiff;
unlock(myLock);
done = true;
barrier(myBarrier, NUM_PROCESSORS);
if (diff/(n*n) >= TOLERANCE)
done = false;
This essentially sets done := true by default and then checks in the if statement if it should be set to false. The difference between this and the given code is that after the second barrier, if diff/(n*n) < TOLERANCE, then each thread skips the new if statement and finishes the while loop. However, if diff/(n*n) >= TOLERANCE, the first thread that encounters the if statement will set done := false, and because the only place done is set to true is between the two barriers in the while loop, all threads will continue on to the next iteration of the while loop even if diff is reset to 0 before they process the if statement, removing the necessity of the last barrier in the original code.
This comment was marked helpful 0 times.

Thinking about spilledmilk's answer, his method is valid assuming that done, stored in global memory somewhere, gets checked by every thread on every access. If done was instead stored in a register I'm not sure it will necessarily work every time. Aside from C's volatile keyword, what other mechanisms for dealing with thread memory accesses/caching are there? (I'm not sure I'm wording my concern properly but hopefully it makes sense.)
This comment was marked helpful 0 times.


Why not use two
diffvariables, instead of 3?This does reduce the synchronization, but it also increases the total amount of work done. Theoretically, the processor would be doing other work on the cores that were stuck at the extra barriers, but now those cores are computing the next iteration, and that work might not ever be needed. Is this a problem? It seems like the code we write here mostly assumes being run in a vacuum since high-performance programs usually have their own machines, so is the fact that it wastes some processor time not important?
This comment was marked helpful 0 times.

@mchoquet: I do not believe this implementation performs any additional work compared to the version on the previous slide.
There may be a more efficient implementation... (if so, let's see it!)
This comment was marked helpful 0 times.

Oh wait, you're right. I misread the code and thought some threads might be able to start doing an unnecessary extra iteration, but that's impossible. I'm still wondering why the diff array has 3 entries instead of 2 though.
This comment was marked helpful 0 times.

@mchoquet: Assume there are two threads consume running right after the barrier. Suppose thread1 is suspended, and thread2 runs just before the barrier. If there are only two diffs, thread2 will zero out the diff thread1 will use to set the conditional variable, and will cause premature termination of thread1.
This comment was marked helpful 4 times.

I think doing it with two diffs and one barrier is impossible by simply reorganizing the logic in this code. Here's my reasoning:
You need a barrier between an update to the current diff and a check of the current diff. If this were not the case, the diff could be checked too early/updated to late and lead to an incorrect result.
Now assume we only have two diffs and one barrier. I've shown the barrier must exist after the update of the diff and before the check of the diff. Somewhere in between those two points must be a zeroing of the next diff. This is where problems are caused.
Review the current state (update current diff) --> barrier --> (check current diff).
We need to insert (zero out diff) before we start using it. If the diff is only used once, we'd have two loops in the while loop and there would be no problem, but we can't assume that.
There are two reasonable ways to insert (zero out diff):
(update current diff) --> barrier --> (check current diff) --> (zero out [next] diff)
and
(zero out [current] diff) --> (update current diff) --> barrier --> (check current diff)
If you put the zero out anywhere else, you'd clearly have a problem. However, both of these cases (which I believe are exhaustive) can screw things up. Observe that they are essentially the same as long as the loop guard does not evaluate to false and consider the second case:
(zero out [current] diff) --> (update current diff) --> barrier --> (check current diff)
Have two threads race from the barrier. Assume one thread just checked the current diff. A second thread at this point has already zeroed out and updated the next diff. Now the first one starts back at the top of the loop. It zeros out the current diff and ruins the result of the second thread.
I think this is general enough to show that as long as there is a "done" state controlled by the "diff" value, you can't just have two diffs and one barrier. However, if the loop guard does some crazy stuff, I'm not sure what is possible. Also the conditional that sets the "done" state could potentially have an accumulator that allows you to reuse diff without zeroing it out, which would solve the main problem I pointed out.
This comment was marked helpful 0 times.


Would this method be less efficient from the processor's perspective than a Barrier? A while loop like that kinda makes me cringe...
This comment was marked helpful 0 times.

@Dave: What specifically makes you cringe? Or in other words, how would you implement barrier(2) in the following code to not make yourself cringe?
Thread 0:
// do stuff to produce x
x = 1;
barrier(2);
Thread 1:
// do stuff here
barrier(2);
print x;
This comment was marked helpful 0 times.

@kayvonf I guess that was really my question, whether barrier is implemented using something other than loops. My reaction to a loop like that may just be an artifact of my Proxylab days, but having to perform millions of checks a second to see if a value has changed seems inefficient. It doesn't sound like such a thing exists, but I was wondering whether modern CPUs might have some gating feature that shuts down a core until the barrier condition is met. Am I wrong about a while(flag==0) loop being taxing on a CPU? Or about how CPUs work? Or both?
This comment was marked helpful 0 times.

You are completely correct, however...
You're taught it is not good to busy wait in other classes because the assumption is that some other process might want the core, and thus the spinning process should be swapped out until the condition it is waiting for is met. However, if you are worried about performance, it's unlikely you're multi-tasking on the machine. If that's the case, and there's nothing else for the core to do, there's potentially no performance loss from spinning. In fact, swapping T1 out so the core sits idle could negatively impact performance since once the flag is set it, it could take much longer for T1 to get placed on the CPU again, increasing the overall time between the flag being set and T1 observing the update.
That said...
- You might not want to busy-wait because busy waiting burns power.
- You might not want to busy-wait in a multi-threaded CPU (e.g., consider a Hyper-threaded situation) because you are burning instruction issue slots that could be used to execute instructions from other hardware threads.
- In light of 1 and 2 above, you might be interested in the implementation of the x86
mwaitandmonitorinstructions. Together they can be used to tell the core to sleep the execution context until a specific condition has occurred, such as a write to a specified memory address. Sounds pretty useful, eh? (Note all this is handled without OS intervention, so the thread is never swapped out of the hardware execution context it is currently assigned to.)
mwait: http://x86.renejeschke.de/html/file_module_x86_id_215.htmlmonitor: http://x86.renejeschke.de/html/file_module_x86_id_175.html- A nice reference from Intel about using
monitorandmwait.
This comment was marked helpful 3 times.

A quick summary of the monitor and mwait instruction: The monitor instruction is used to define a memory range starting at the address specified in eax. The width of the monitored area is on a per CPU basis and can be checked with the cpuid instruction. Once the monitor instruction has been executed, the mwait instruction can then be used to enter an "implementation dependent optimized state" and execution will not resume until a write to the monitored address range or an interrupt occurs. Various other parameters to both mwait and monitor can be passed in other registers.
This comment was marked helpful 2 times.


The amount of communication that needs to happen is proportional to the perimeter of each chunk of cells. In this example, there are 4 chunks being computed by 4 threads, and each has to send/receive the top and bottom row at every timestep (except for the very first and last rows). As was mentioned in class, a more efficient way to break up this problem would be to make a 2-dimensional grid of chunks because square chunks minimize the perimeter-to-area ratio.
This comment was marked helpful 0 times.


I think the communication is performed en masse because there is a cost associated with sending messages, and sending by row instead of by element cuts down on the extra costs of message passing.
On that note, performance-wise, how does the message passing model compare to the other models? It would seem as though it would be slower.
This comment was marked helpful 0 times.

@bstan I believe there are some VM tricks that can be applied to speed up message passing, but that is essentially shared address space model. I think message passing is slower compared to other models too as there may be lots of copying and synchronization. Wonder if there is any special hardware support for this kind of model.
This comment was marked helpful 0 times.

I think an example of message passing using VM tricks is to mmap a region of memory, write into it, then somehow tell another process to also map that memory, so it can read/write to it. That does sound a lot like shared address space though...
I suppose this could also be done with pipes, but in that case the OS is probably doing copying between buffers.
This comment was marked helpful 0 times.

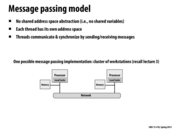
As another perspective, Message Passing is designed as a way to facilitate parallel processing on heterogeneous distributed systems with distributed memory. Applications that use it are probably designed to have minimal use of shared data and do most of their computation on local memory, with communication via small-sized sends/receives over the network. It doesn't seem like you can improve upon this model by implementing a shared address space, since that really is just a layer of abstraction, and would require additional synchronization that would still at the low level be implemented by point-to-point sends and receives.
This comment was marked helpful 0 times.

I am sure message passing has some overhead in establishing a connection before actual data is exchanged. In this we want to minimize that overhead by doing communication en masse.
This comment was marked helpful 0 times.


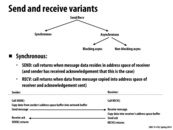
Each of the processes are trying to send, but the send calls won't get to return because none of the processes are receiving. Will the deadlock still happen if we moved up line 16d to before line 16b?
Can't seem to remember, was this slide (and those following) covered in lecture?
This comment was marked helpful 0 times.

@eatnow I think that still might deadlock since then all the threads will be waiting for RECEIVE to return, but no one has sent any messages. If we still wanted to use blocking calls, we can probably just have thread 0 be the master initially and send out all the necessary data to threads 1, 2, ... nprocs - 1. I'm not sure whether this has significant performance implications, since majority of the cost is probably in the main computation itself rather then copying of data.
This comment was marked helpful 0 times.

@eatnow I am beginning to believe that you're right. If you moved up line 16d, then I think what would happen is all pid's except for 0 would send, and 0 would go to receive. 0 would receive from 1, and then 1 would go receive from 2, and so on. Once these are all done, all pid's from 0 to nprocs-1 will be sending, and nprocs-1 will be the first to receive. It will receive from nprocs-2, which will then go receive from nprocs-3, all the way down to 0. The problem with this is that this is basically sequential. Other solutions such as having even and odd numbered rows taking turns sending and receiving would be more parallel.
This comment was marked helpful 1 times.
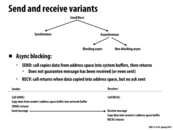

It seems to me that blocking send and receive are only useful when you already know which will be sending and which will be receiving. Since both does not return unless data is completely sent/received, it feels like work needs to be specified clearly for all the processors.
This comment was marked helpful 0 times.
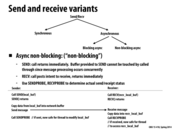

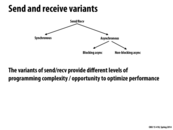
The one downside of the two variants presented in the previous slides is that they must wait for the copy of data into the network buffer to complete. So I think one reason to use async non-blocking is when a routine has to complete its task within a very short time frame. If this routine were to use async blocking, it might take too long if the data being sent was big.
I see two challenges to using async non-blocking. First is that there needs to be some sort of synchronization code to ensure that "nothing bad happens". (Concurrent SEND, modifying the buffer specified by SEND, etc). In the two other variants, the synchronization was happening within SEND and RECV. But in async non-blocking, this needs to happen outside of SEND and RECV.
The second challenge is that there needs to be some thread/task/worker that actually handles the copying of data specified by SEND into the network buffer. And there are other related issues, such as when and who spawns this worker, and how they are scheduled.
This comment was marked helpful 0 times.


I'm still a bit confused between data-parallel and shared address space. It seems that data-parallel does sometimes involve loads and stores on a shared address space (like in the example on slide 30). Is the only difference in the synchronization, as in forall handles the assignment and synchronization while in shared address space each "thread" is responsible for finding its own assignment (through something like threadId)?
This comment was marked helpful 0 times.

Great question! I wouldn't pull hairs about the differences because many real programming frameworks are combinations of these ideas, but there are some clear differences in how one thinks about how to express a program in each model. What might those be? One similarity is that both the data-parallel ("streaming") and shared address space models, in the simple form I talked about here, adopt a single global shared address space.
This comment was marked helpful 0 times.





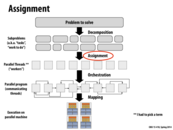
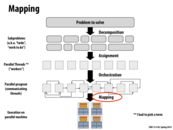













Hint. Professors don't enjoy apples for treats. They enjoy comments that provide new music suggestions. (But only if they are justified in terms of their relationship to course topics.)
This comment was marked helpful 0 times.
Uh maybe Parallel Universe - RHCP?
This comment was marked helpful 0 times.